Examples of Scientific Demonstration
We begin this section with examples from mathematics, because these are always simpler and clearer than in other sciences. We give one from arithmetic which is so simple as to appear entirely trivial, but it illustrates a method which is the same for every arithmetical or algebraic proof, no matter how complicated it may be.
Theorem: Any odd number minus 1 is equal to some even number.
Proof:
The sum of two equal numbers is an even number. And: every odd number minus 1 is the sum of two equal numbers. Therefore: every odd number minus 1 is an even number.Major: This is a definition of an even number, namely, "A number is even which can be divided into two equal and largest parts."
Minor: This is the definition of an odd number, namely, "All odd number is one which cannot be divided into two equal and largest parts without the remainder of a unit."
This is a strict proof since:
- It is in correct syllogistic form (namely Barbara).
- The premises are universal, necessary, and evident because they are real
definitions. In arithmetic We postulate the existence of the unit and of numbers, as we
have seen, and by these we can prove the existence of any natural number. It is easy to
prove that there are even numbers, for example, 2. Then the present demonstration
amounts to a proof of the existence of odd numbers,
Someone might object that 1 is neither odd nor even; but as we have seen, 1 is not a number.
- It is through the proper formal cause, since it is made through the definition of the two kinds of numbers.
Theorem: If two straight lines AB and CD cut one another, the vertical or opposite angles a and b are equal:
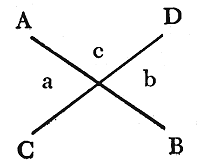
Proof: (Premises marked with an asterisk* are proved below): 1* The remainders of equals minus equals are equal. 2* And: every pair of vertical angles (such as a and b) are the remainders of equals minus equals. Therefore: every pair of vertical angles are equal.
Proof of 1* : This is an axiom (it means the same is, "If equals are subtracted from equals, the remainders are equal).
Proof of 2* :
4*. Remainders of a plus c,
and b plus c, each minus c are remainders of equals minus equals.
5*. And: vertical angles a and b are the remainders of a plus c, and b
plus c, each minus c.
2*. Therefore: vertical angles
a and b are remainders of equals minus equals.
- Proof of 4.*: It is evident that angle c is "equal" to itself, but it remains to be proved that a plus c, and b plus c, are equal.
- 6.* Every straight angle is equal to every other.
- 7.* And: a plus b and b plus c are straight angles.
- 4.* Therefore: a plus b and b plus c are equal.
- 6.* This is a previous theorem, namely, that "The angles which one straight line makes with another straight line on one side of it are equal to two right angles (i.e., a straight angle). We omit this proof.
- 7.* And: a plus b and b plus c are straight angles.
- Proof of 5*: This is evident from the definition of vertical angles.
This also is a strict proof, because:
- It is in correct syllogistic form.
- The ultimate premises are all axioms, definitions, or postulates (except 6*, which can also be proved by these same axioms, definitions, and postulates).
- It is through the proper reason, because the middle term in the first syllogism is "the remainders of equals minus equals" which is the cause of a and b being equal, since their size is determined by the overlapping of two straight angles of which they are remainders.
In this handbook we have studied logic as an art, learning its rules and practicing their application to various kinds of materials. How do we know that these rules themselves are true? Logic is not only an art, but it is also a science which proves its own rules.
The following demonstration taken from Aristotle's Posterior Analytics is the most important rule of all of logic, since it tells us how to form a scientific demonstration. Aristotle explains this demonstration at great length, and we give it here only in abbreviated form. The various premises which require to be proved are numbered in order with an asterisk, thus 1*.
1*. An argument giving us knowledge
of the cause on which some fact
depends as its proper cause so that
the fact cannot be otherwise is a syllogism whose premises
contain a real essential definition
(or its equivalent) of the subject
as cause of its properties.
2. And: a scientific demonstration is an argument giving us knowledge
of, etc.
Therefore:
a scientific demonstration is a syllogism whose premises
contain a real essential definition
(or its equivalent) of the subject
as cause of its properties.
Proof of 1*: Two parts.
a. It is a syllogism, because an argument is either an induction or a syllogism. But only a syllogism has a universal middle term, and hence only a syllogism can give the necessary cause why a fact cannot be other than it is.
That a syllogism is valid is shown below, page 570.
b.
3*. Premises which are true, primary,
indemonstrable, and also prior to,
more known than, and the cause
of the conclusion are ones which contain a real
essential definition (or its
equivalent) of a subject as the
cause of its properties.
4*. an argument giving us knowledge
of the cause on which some fact
depends as its proper cause so that
the fact cannot be otherwise is one whose premises are true,
primary, etc.
1.* Therefore: an argument giving
us knowledge of the cause on which
some fact depends as its proper cause
so that the facts cannot be otherwise is one whose premises contain a
real essential definition of a
subject as the cause of its
properties.
Proof of 3*: A statement is seen to be true, primary, and indemonstrable when it is evidently true from the very meaning of the terms, where no intermediate term is needed nor possible. This is the case only when the one term is the essential definition of the other, or so closely connected with it as to be equivalent to a definition. But if this is to give scientific knowledge it must also be a real definition. Furthermore, it is only this nature which is prior to and the cause of the properties of the thing. We arrive at the nature by definition, and this is found by observation and classification, not by demonstration. Hence in itself the definition is better known than the properties.Proof of 4*: A scientific demonstration must have premises which satisfy these six conditions, for the following reasons: They must be:
1) true, since only a true premise could cause true knowledge.
2) primary, since otherwise they would depend on previous truths.
3) indemonstrable, because eventually we must get to immediately evident truths.
4) prior, since the conclusion depends on them.
5) better known than the conclusion, since through them we know the conclusion :
6) cause of the conclusion, since science is perfect knowledge, and we have this only when we know both the fact and its proper cause.
We have assumed in the above argument (1.*a) that a syllogism is a valid argument, and in fact we had to use a syllogism in order to prove the above conclusion. Hence we must be sure that the syllogism is valid. This cannot be demonstrated, since it would be circular to prove that a syllogism is valid by using a syllogism.
Aristotle in the Prior Analytics shows how we can establish the validity of the syllogism in the First Figure, not by a demonstration, but by showing it is an application of the principle of contradiction. Then we can establish the validity of the other forms of the syllogism by reducing them to the First Figure:
A. There are eight general laws of the valid syllogism, as follows:
1. There can only be three terms.
2. The middle term must be a distributive universal at least once see page 75).
3. Both premises cannot be negative.
4. Both premises cannot be particular.
Reason: These rules follow from the definition of the syllogism, since if there are more than three terms, or if the extremes are not connected by the middle term, this definition is violated.
5. The conclusion cannot be wider in extension than the premises.
6. The middle cannot be in the conclusion.
7. The conclusion cannot be stronger than the weakest premise.
8. Affirmatives cannot give a negative conclusion.
Reason: These rules are based on the axiom, common to all sciences, that a cause
must contain its effect, since if any of these rules are violated the conclusion of the
syllogism, which is an effect of the premises, will contain something that the
premises do not contain.
B. There are three possible figures of the syllogism:
- First Figure in which the middle term is once a predicate and once a subject in the premises.
- Second Figure in which the middle term is a predicate in both premises.
- Third Figure in which the middle term is a subject in both premises.
C. Each of these figures has special laws, based on the general laws above, as follows:
(NOTE: To understand the following proofs, we must recall that in affirmative statements the predicate is taken particularly, while in negative statements it is taken universally. Thus when we say "Every man is an animal," we do not imply that "Every animal is a man"; but when we say "No man is an angel" we do imply that "Every angel is not a man.")
1. Law of First Figure: The major must be universal and the minor affirmative.
Proof:
- 1) Minor must be affirmative, for if it were negative, then
- a) Either the major would also be negative and this violates general law 3 above;
- b) Or the major would be affirmative, and then the major term being in predicate position in this figure would be particular, while in the conclusion it would be universal, because the conclusion would be negative (general law 7), and this would violate general law 5.
- 2) Major must always be universal. Since we have just proved that the minor is affirmative, its predicate is particular; this predicate is the middle term, which is thus undistributed in the minor premise. Since the middle term must be distributed in one premise (general law 2), it must be distributed in the major premise, where it is the subject. Hence the major premise must be universal.
2. Law of the Second Figure: The major must be universal and one premise negative.
Proof:
- 1) If both premises were affirmative, the middle would not be distributed since it is in the predicate place in both premises and is therefore particular.
- 2) The major must be universal since we have just proved that one premise is negative, and hence that the conclusion is negative (general law 7); hence the major term is universal in the conclusion and must be universal in the premises (general law 5).
3. Law of the Third Figure: The minor must be affirmative and one premise universal.
Proof:
1) One premise must be universal (general law 4).
- 2) The minor must be affirmative. If it were negative, then the conclusion must be negative (general law 7), and its predicate, which is the major term, will be universal; hence it will also be universal as the predicate of the major premise (general law 5). Then this major premise must be negative, and both premises would be negative, which violates general law 3. Hence the minor must be affirmative.
There are four possible kinds of statements, A,E,I,O (see page 70), and there are three possible figures, as we have just shown. Hence we can have 4 x 4 x 3, or 48, possible combinations of premises. The following table shows why some forms are invalid. The names given to the possibly valid forms are memory words chosen so that the vowels indicate the kinds of propositions which make up the premises and the conclusion. Thus "Barbara" is the name of a syllogism made of three A propositions; "Celarent" is the name of a syllogism made of EAE propositions; etc.
FIRST FIGURE: Rule: Major must be universal, minor affirmative.
| 1. AA Barbara | 9. IA major particular |
| 2. AE minor negative | 10. IE major particular, minor negative |
| 3. AI Darii | 11. II major particular |
| 4. AO minor negative | 12. IO major particular, minor negative |
| 5. EA Celarent | 13. OA major particular |
| 6. EE minor negative | 14. OE major particular, minor negative |
| 7. EI Ferio | 15. OI major particular |
| 8. EO minor negative | 16. OO major particular, minor negative |
SECOND FIGURE: Rule: Major must be universal, one premise negative.
| 17. AA both premises affirmative | 25. IA major particular, both affirmative |
| 18. AE Camestres | 26. IE major particular |
| 19. AI both premises affirmative | 27. II major particular, both affirmative |
| 20. AO Baroco | 28. IO major particular |
| 21. EA Cesare | 29. OA major particular |
| 22. EE both premises negative | 30. OE major particular, both negative |
| 23. EI Festino | 31. OI major particular |
| 24. EO both premises negative | 32. OO major particular, both negative |
THIRD FIGURE: Rule: Minor must be affirmative, one premise universal.
| 33. AA Darapti | 42. IE minor negative |
| 34. AE minor negative | 43. II both particular |
| 35. AI Datisi | 44. IO minor negative, both particular |
| 36. AO minor negative | 45. OA Bocardo |
| 37. EA Felapton | 46. OE minor negative |
| 38. EE minor negative | 47. OI both particular |
| 39. El Ferison | 48. OO minor negative, both particular |
| 40. EO minor negative | |
| 41. IA Disamis |
E. Next we show that these syllogisms in the Third and Second Figure are equivalent to ones in the First Figure, by reducing them. We can do this by the following operations:
- 1) We can simply convert (symbolized by s) E and I propositions. This means simply
to exchange the subject and predicate. We can do this because in E and I propositions
the predicate is no wider in extension than the subject. If it were, then conversion
would change the truth of the statement. We cannot convert "Every man is an animal"
(A) but we can convert "Some man is an animal" (1), without changing the truth of the
statement.
- 2) We can convert and make particular (symbolized by p) an A preposition.
- 3) We can exchange (symbolized by m for "mutate") the premises, since this makes no essential difference to an argument.
- 4) We can prove by reducing to absurdity the contradiction of a conclusion (symbolized by c). Thus we can take the conclusion of the syllogism whose validity we wish to establish, and then contradict it. Using this contradiction as a major premise, and taking the minor premise of the original syllogism, we can form a new syllogism, whose conclusion will be the contradictory of the original major premise. Thus it is absurd to deny the validity of the original syllogism, since such a denial leads to a contradiction of the original premises.
- 2) We can convert and make particular (symbolized by p) an A preposition.
If we apply these four processes to the syllogisms left over from D, we find that they can all be reduced to syllogisms in the first figure.
The consonants in the memory-names tell us bow to do this. Those which begin with B
can be reduced to Barbara, those beginning with C to Celarent, etc., if we perform the
operation on a proposition symbolized by the consonant which follows it. Thus in Cesare
we take the first E proposition and simply convert it (c E s are). Consonants other than the
ones given above have no significance.
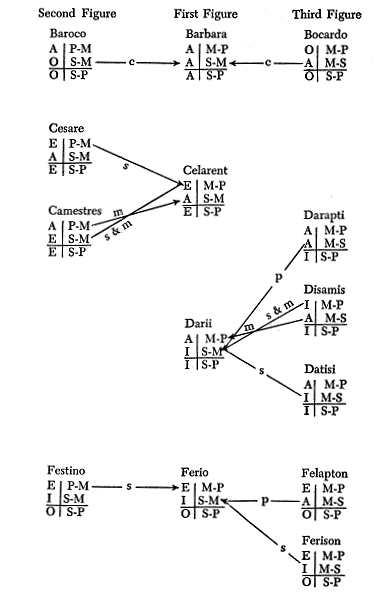
F. Now how can we be sure that the four syllogisms in the First Figure, namely, Barbara, Celarent, Darii, and Ferio, are valid?
- 1. Obviously Darii and Ferio are valid if Barbara and Celarent are valid, since they are respectively only weaker forms of the latter.
- 2. Proof that Barbara and Celarent are valid:
- a. These two modes are a simple application of the following principle (called in Latin the dictum de omni et de nullo, "what is said of all and of none"):
- Whatever (P) is universally distributively affirmed of some subject (M) ought to be affirmed of everything contained under its extension (S); and whatever is universally distributively denied of some subject ought to be denied of everything contained under its extension.
- b. And this principle is only a special case of the broader principle (called the principle of agreement and disagreement):
- Whenever two things are the same as one third thing they are the same as each other; and whenever of two things one is the same as a third thing, and the other is not the same as this third thing, they are not the same as each other.
- c. This principle of agreement and disagreement must be true, because if we assume its contradictory, we violate the principle of contradiction (namely, that a thing cannot both be and not be at the same time and in the same respect), as follows:
- If two things were the same as a third thing, and not the same as each other, then they would be X (the third thing) and not be X (since each is the same as X, but they are Dot the same as each other) at the same time, and in the same respect (with respect to X).
- d. The principle of contradiction is true, because it is the first principle of all knowledge, which men cannot doubt in their minds, although they may say they doubt it.
Thus we have reduced the valid forms of the syllogism to the most solid possible basis. If these forms are not valid, then the principle of contradiction is not valid, and all knowledge is impossible.
G. The following are examples of the valid forms of the syllogism. It will be noted that:
- 1. The First Figure in Barbara alone can give universal affirmative conclusions.
Hence only Barbara can give us a perfect scientific demonstration.
- 2. The Second Figure is useful for refuting others because it always yields a negative conclusion.
- 3. The Third Figure is also useful in refutation by proving an exception to a statement, since it always ends particularly.
- 2. The Second Figure is useful for refuting others because it always yields a negative conclusion.
BENJAMIN FRANKLIN AND THE NATURE OF LIGHTNING
The following is from a letter of Franklin to John Lining, written in 1755:
"Your question, how I came first to think of proposing the experiment of drawing down the lightning, in order to ascertain its sameness with the electric fluid, I cannot answer better than by giving you an extract from the minutes I used to keep of the experiments I made, with memorandums of such as I proposed to make, the reasons for making them, and the observations that arose upon them, from which minutes my letters were afterwards drawn. By this extract you will see, that the thought was not so much "an out-of-the-way one," but that it might have occurred to any electrician.
'November 7, 1749. Electrical fluid agrees with lightning in these particulars. (1) Giving light. (2) Colour of the light. (3) Crooked direction (4) Swift motion. (5) Being conducted by metals. (6) Crack or noise in exploding. (7) Subsisting in water or ice. (8) Rending bodies it passes through. (9) Destroying animals. (10) Melting metals. (11) Firing inflammable substances. (12) Sulphurous smell. The electric fluid is attracted by points. We do not know whether this property is in lightning. But since they agree in all particulars wherein we can already compare them, is it not probable they agree likewise in this? Let the experiment be made. . . .'"
The following is from a letter to Peter Collinson, written earlier in 1752:
" As frequent mention is made in public papers from Europe of the success of the Philadelphia experiment for drawing the electric fire from the clouds by means of pointed rods of iron erected on high buildings, and it may be agreeable to the curious to be informed that the same experiment has succeeded in Philadelphia, though made in a different and more easy manner, which is as follows:* [* Franklin was lucky in his experiments. Many people have been killed trying to reduplicate these experiments. No student should attempt them, as they are extremely dangerous.]
Make a small cross of two light strips of cedar, the arms so long as to reach the four corners of a large thin handkerchief when extended; tie the corners of the handkerchief to the extremities of the cross, so you have the body of a kite; which being properly accommodated with a tail, loop, and string, will rise in the air, like those made of paper; but this being of silk, is fitter to bear the wet and wind of a thundergust without tearing. To the top of the upright cross is to be fixed a very sharp pointed wire, rising a foot or more above the wood. To the end of the twine, next the hand, is to be tied a silk ribbon, so that where the silk and twine join a key may be fastened. This kite is to be raised when a thundergust appears to be coming on, and the person who holds the string must stand within a door or window or under some cover, so that the silk ribbon may not be wet; and care must be taken that the twine does not touch the frame of the door or window. As soon as any of the under-clouds come over the kite, the pointed wire will draw the electric fire from them and the kite, with all the twine, will be electrified, and the loose filaments of the twine will stand out every way, and be attracted by an approaching finger. And when the rain has wet the kite and twine, so that it can conduct the electric fire freely, you will find it stream out plentifully from the key on the approach of your knuckle. At this key the phial may be charged; and from the electric fire thus obtained, spirits may be kindled, and all the other electric experiments performed, which are usually done by the help of a rubbed, glass rod or tube, and thereby the sameness of the electric matter with that of lightning completely demonstrated."
Analysis:
- A. The first quotation is an excellent example of dialectical reasoning in which Franklin is seeking a definition of lightning in terms of its material cause by comparing it (similarities and differences) with something better known, namely, the "electrical fluid" used in laboratory experiments.
- 1. He lists 12 similarities. Notice that they relate to qualities (light, color, shape, sound, smell), to its motion, and its action (passes through metals and ice, rends bodies, kindles fuels, melts metals).
- 2. He notes one possible difference, not yet tested: "electric fluid" is attracted by points. (When it had been established that this was true also of lightning, the way was opened to the invention of the lightning rod).
- Since the identity of the two things seems probable, Franklin frames a hypothesis: Lightning is composed of electric fluid. This is a tentative definition of lightning in terms of its material cause.
- B. This hypothesis now has to be tested:
Franklin carefully describes his apparatus and the manner of performing the experiment. Although this apparatus was quite crude, nevertheless his description makes it possible to repeat his experiment and thereby to generalize (induction) from its result.
In this case the experiment did not merely confirm the hypothesis as probable, but rendered it truly certain, since once lightning bad been "captured" in this way it became possible to test it repeatedly for all the characteristic properties of "electrical fluid" and therefore to be sure that they are identical. Here we have an example of how dialectical reasoning prepares the way for an observation from which a real definition (not merely a tentative one) can be obtained. Such a definition is certain, not from demonstration, but from immediate evidence.
- C. Once this real definition bad been established by Franklin, then it became possible to demonstrate some of the properties of lightning with certitude. For example, we might form the following demonstration, as Franklin actually did in inventing the lightning rod:
An electrical discharge tends to pass more easily through a pointed metal conductor. And: lightning is an electrical discharge. Therefore: lightning tends to pass more easily through a pointed metal conductor.Major: This had already been shown by laboratory experiments with electrical fluid.Minor: This is what Franklin had first guessed at dialectically, and then established with certitude from observation. It is a definition, although an incomplete one, of lightning.
THE LAW OF LEVERS
The following is a typical practical problem which can be solved by elementary mechanics:
Problem: A log 11 feet long is used as a first-class lever (see diagram) to lift the wheel of an automobile out of the mud. The wheel is supporting 1500 pounds weight. The fulcrum of the lever is placed 1 foot from the axle, and the axle is at the end of the log to lift stands on the other end of the log. How heavy must he be wheel?
|
RF: resistance arm EF: effort arm DI: distance moved by applied effort
D2: distance moved by weight to be lifted | 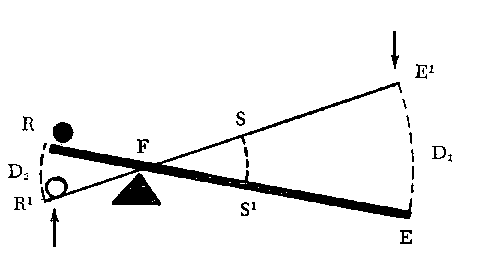 |
Answer:
1: ideal mechanical advantage M = EF = 10 feet = 10
RF 1 foot
2. ideal effort required E = resistance R = 1500 = 150 lbs. (the man's weight).
ideal M 10
The problem is only an individual case of a general law, namely:
ideal M = D1 = EF
D2 RF
The student is likely merely to learn such a formula and apply it to problems in a routine fashion. A scientist however is not so much concerned with working problems as understanding the reason why.
How do we know that this law is true?
The law as a general fact: This law of the first class lever can be tested experimentally and found to be approximately true. That is why we say "ideal mechanical advantage" because in actual experimentation various factors interfere with its being perfectly
realized, and the lever is found not to be quite as effective as the law would predict. However, we can be sure that the law is true in every case within very narrow limits, and by removing disturbing factors we can make this accuracy greater and greater.
The reason for this fact: This can be stated in syllogistic form as follows:
The ratio of arcs RR' and EE' is equal to the ratio of the
distances EF and RF
And: in a lever the ideal
mechanical advantage is equal to ratio of the distances
moved by the effort and the
resistance, i.e., the ratio
of arcs RR' and EE'
Therefore: in a lever the
ideal mechanical advantage is equal to the ratio of the distances
EF and RF,i.e., to the ratio of
the effort and the resistance arm.
Major: This is a theorem which can be proved in geometry. It applies in the present case, because the angles RFR' and EFE' are equal (they are vertical angles). Hence it is possible to lay off the distance FS and FS' equal to FR and FR' and then the arc SS' will be equivalent to the arc RR'. Then it is easy to prove that the arcs within this segment of a circle have the same ratio as their radii, namely, that SSI: EEI : : FS: FE'.Minor: This is a nominal definition of "mechanical advantage" and is based on the physical fact that a small amount of energy will move a large body through a small distance.
It will be noticed that in this proof the major premise is purely mathematical and rests on mathematical axioms and postulates. The minor, on the other band, is purely physical, since it deals with the characteristics of moving bodies. The middle term is common to both. In the major premise it is taken in the sense of a relation between abstract quantities, in the minor premise as a measurement of concrete or physical quantities, since the distances spoken of are physical distances through which physical bodies are moved by physical forces. The application of mathematics to physics takes place in the conclusion, which states a physical law in mathematical terms.
This demonstration is through a proper cause from the mathematical point of view, since the proper cause for this equality of proportion is the equal angle of the arcs.
HARVEY'S PROOF OF THE CIRCULATION OF THE BLOOD
William Harvey (1578-1657) corrected the most serious mistake of Greek and medieval biology, the wrong conception of the function of the heart. His proof that the true function of the heart is to circulate the blood opened the way to the whole modern development of physiology, which is the basic part of biology. Consequently, Harvey is sometimes pictured as a scientific revolutionary. In fact the opposite is the case; his work is a proof of the continuity between ancient and modern biology, since Harvey was a thorough Aristotelian. He had learned the Aristotelian method of accurate observation and acute reasoning during his studies at the University of Padua, the stronghold of Aristotelian science in Europe, and this method is beautifully exemplified in his great work, An Anatomical Disquisition on the Motion of the Heart and the Blood in Animals.
The student who wishes to understand the scientific method should study this work carefully. He will find that it is a very clear example of a complete exposition, as the following outline indicates (compare with pages 185 ff).
- A. Statement of the question:
1. Introduction: Reviewing opinions of previous writers about the pulse and function of the arteries and the heart, Harvey shows that these opinions leave serious problems unsolved.
- CHAPTER I: Why the author is writing; the difficulty of the subject, etc.
- Harvey uses his introduction, which is quite lengthy, to give a historical account of the opinions held before his time. Then be uses Chapter I to give a rhetorical introduction in which he wins the favor, attention, and interest of his reader. We might have expected the reverse order, but Harvey well realized that nothing would better establish himself with his readers, who were professional medical men and biologists, than to show his thorough acquaintance with the whole history of the problem. Only after this does he then attempt a more formal beginning. This is an example of the way in which the form of a complete exposition can be varied and adapted to different circumstances.
- 2. Search for a definition of the heart:
- CHAPTER II: The motion of the heart as observed in animal experiments.
- CHAPTER III: The motion of the arteries as observed in animal experiments.
- CHAPTER IV. The motion, action, and function of the heart: a summary of what has been shown in the preceding chapters. The definition of the heart arrived at is as follows:
"The chief function of the heart is the transmission and pumping of blood through the arteries to the extremities of the body. Thus the pulse which we feel in the arteries is nothing else than the impact of blood from the heart."
- CHAPTER III: The motion of the arteries as observed in animal experiments.
- This still pertains to the state of the question, because it consists in stating the
principle by which a solution to the problem can be reached, namely, a definition of the
heart. Definitions are not demonstrated, but can be arrived at only by an analysis of
experience; hence Harvey carefully prepares the way for his definition by a series of
beautiful experiments in which false definitions are eliminated, and the true one exposed.
The definition arrived at is in terms of the four causes, since (as the student can verify
from the text of Harvey's work) he establishes the composition, structure, and function of
the heart (i.e., its material, formal, and final causes). The efficient cause of the heart is not
treated in detail in this work, as it is a problem of embryology which Harvey develops in
another famous book. Furthermore, Harvey makes clear that he does not suppose his
definition to be complete, since he is not sure whether the heart is only a pump, or whether
in addition to this it acts on the blood chemically. This latter problem be leaves for further
study, and indeed it can not be solved until much later when the nature of oxidation has
been discovered by chemists. He has defined the heart as a pump, but he has not yet
proved that it is a property of the pump to circulate the blood.
- B. The Demonstration:
- CHAPTER VI: The course by which the blood is carried from the vena cava into the
arteries, or from the right into the left ventricle of the heart.
- CHAPTER VII: The blood percolates through the substance of the lungs from the right ventricle of the heart into the pulmonary veins and the left ventricle.
- CHAPTER VIII: How Harvey came to discover the circulation of the blood.
- CHAPTER IX: The formal demonstration of the circulation of the blood.
- CHAPTER X: The first proposition presupposed in this proof freed from objections and confirmed by experiments. Here Harvey shows that the heart pumps too much blood into the arteries for this blood to be newly made.
- CHAPTER XI: The second proposition presupposed is defined. Here Harvey shows that the blood in the arteries is too great to have been newly made.
- CHAPTER XII: Shows that, from the forgoing two premises, circulation is a necessary conclusion.
- CHAPTER XIII: A third proposition implied in the proof, namely, the veins bring the blood back to the heart.
- CHAPTER XIV: Final statement of his conclusion, namely, that circulation is proper to the blood and the heart.
- CHAPTER VII: The blood percolates through the substance of the lungs from the right ventricle of the heart into the pulmonary veins and the left ventricle.
- C. Confirmation of the demonstration:
- CHAPTER XV: The proof is confirmed by plausible arguments.
- CHAPTER XVI: The proof is confirmed by comparative anatomy.
- It will be noticed that in giving his demonstration Harvey first gives a dialectical
preparation for it in Chapters VI-VIII. The first two of these chapters remove the chief
difficulty to understanding his proof, namely, certain mistaken ideas about the relation of
the lungs to the heart. Chapter VIII tells how Harvey hit on the idea of circulation,
namely, from the analogy between the vascular system and cyclical processes in non-living
nature.
Next Harvey gives his proof in short form in Chapter IX, and then proceeds to establish the premises on which the proof is based. The major premise is immediately evident, but the minor premise presupposes three other statements, and these Harvey establishes in Chapters X to XIII. Then in Chapter XIV he actually puts together his complete proof, as follows:
CHAPTER XIV (in the translation from Latin of Robert Willis)
And now I may be allowed to give in brief my view of the circulation of the blood, and to propose it for general adoption.
Since all things, both argument and ocular experience, show that the blood passes through the lungs and heart by the action of the ventricles, and is sent for distribution to all parts of the body, where it makes its way into the veins and pores of the flesh, and then flows by the veins from the circumference on every side to the center, from the lesser to the greater veins, and is by them finally discharged into the vena cava and right auricle of the heart, and this in a quantity or in such flux and reflux thither by the arteries, hither by the veins, as cannot possibly be supplied by the ingested food, and is much greater than can be required for mere purposes of nutrition; it is necessary to conclude that the blood in the animal body is impelled in a circle, and is in a state of ceaseless motion; that this is the act or function which the heart performs by means of its pulse; and that it is the sole and only end of the motion and contraction of the heart.
We may formulate this demonstration of Harvey's in the following syllogism:
An organ which pumps to the body a much greater quantity of blood than can be supplied by the food eaten is a pump to circulate the blood. And: the heart is such an organ. Therefore: the heart is a pump to circulate the blood.
- Major: This is evident from the general principles of physics, which show that there are only two simple types of motion, that in a straight line, and that in a circle, or closed line.
- Minor: That the heart is such an organ can be establish from three propositions:
- 1. Too much blood leaves the heart to be produced from food in a single day. This can be seen from the capacity of the heart, the number of beats per minute and its structure as a pump.
- 2. Too much blood leaves the arteries to be produced from food in a single day; shown in a similar way.
- 3. The same amount of blood is returned by the veins to the heart.
It will be noticed that this proof depends on the quantity of blood, but nevertheless is not a mathematical-physical proof, since what is involved is not an exact quantity, nor any special property of quantity, but merely a rough proportion, as can be seen from the very round figures which Harvey uses.
Harvey does not give a special section of his exposition to answering objections because be finds it more convenient to take up these objections chapter by chapter, but he does confirm his proof by a series of arguments which are plausible, but which do not give the proper reason for his conclusion. In his main proof the proper reason assigned is from the material cause (the quantity of blood), but it also involves the formal cause, since Harvey has already established that the structure of the heart is obviously pump-like.
LEO XIII ON THE RIGHT OF PRIVATE PROPERTY
The following is part of the argument for the natural right of private property given by Leo XIII in his great encyclical, Rerum Novarum (1891), in which he refutes the theories of socialism and proposes the Christian doctrine on the rights of labor.
For every man has by nature the right to possess property as his own. This is one of the chief points of distinction between man and the animal creation. For the brute has no power of self-direction, but is governed by two chief instincts, which keep his powers alert, move him to use his strength, and determine him to action without the power of choice. These instincts are self-preservation and the propagation of the species. Both can attain their purpose by means of things which are close at hand; beyond their surroundings the brute creation cannot go, for they are moved to action by sensibility alone, and by the things which sense perceives. But with man it is different indeed. He possesses, on the one band, the full perfection of animal nature, and therefore he enjoys, at least as much as the rest of the animal race, the fruition of the things of the body. But animality, however perfect, is far from being the whole of humanity, and is indeed humanity's humble handmaid, made to serve and obey. It is the mind, or the reason, which is the chief thing in us who are human beings; it is this which makes a human being human, and distinguishes him essentially and completely from the brute. And on this account -- viz., that man alone among animals possesses reason -- it must be within his right to have things not merely for temporary and momentary use, as other living beings have them, but in stable and permanent possession; he must have not only things which perish in the using, but also those which, though used, remain for use in the future.
This becomes still more clearly evident if we consider man's nature a little more deeply. For man, comprehending by the power of his reason, things innumerable, and joining the future with the present-being, moreover, the master of his own acts-governs himself by the foresights of his counsel, under the eternal law and the power of God, whose Providence governs all things. Wherefore it is in his power to exercise his choice not only on things which regard his present welfare, but also on those which will be for his advantage in time to come. Hence man not only can possess the fruits of the earth, but also the earth itself; for of the products of the earth be can make provision for the future. Man's needs do not die out, but recur; satisfied today, they demand new supplies tomorrow. Nature, therefore, owes to man a storehouse that shall never fail, the daily supply of his daily wants. And this he finds only in the inexhaustible fertility of the earth.
Nor must we, at this stage, have recourse to the State. Man is older than the State and he holds the right of providing for the life of his body prior to the formation of any State.
And to say that God has given the earth to the use and enjoyment of the universal human race is not to deny that there can be private property. For God has granted the earth to mankind in general; not in the sense that all without distinction can deal with it as they please, but rather that no part of it has been assigned to any one in particular, and that the limits of private possession have been left to be fixed by man's own industry and the laws of individual peoples. Moreover, the earth, though divided among private owners, ceases not thereby to minister to the needs of all; for there is no one who does not live on what the land brings forth. Those who do not possess the soil, contribute their labor; so that it may be truly said that all human subsistence is derived either from labor on one's own land, or from some laborious industry which is paid either in the produce of the land itself or in that which is exchanged for what the land brings forth.
Here, again, we have another proof that private ownership is according to nature's law. For that which is required for the preservation of life and for life's well being, is produced in great abundance by the earth, but not until man has brought it into cultivation and lavished upon it his care and skill. Now, when man thus spends the industry of his mind and the strength of his body in procuring the fruits of nature, by that act he makes his own that portion of nature's field which he cultivates -- that portion on which he leaves, as it were, the impress of his own personality; and it cannot but be just that he should possess that portion as his own, and should have a right to keep it without molestation....
The principal argument of this selection may be formulated as follows:
A rational animal is endowed by nature with the right to
possess permanent private property.
And: man is a rational animal.
Therefore: man is endowed by nature with the right to
possess permanent private property.
Proof of Major:
An animal which must
deliberately provide for
its future material needs is endowed by nature with the right to
possess permanent private property.
And: a rational animal is an animal which must deliberately
provide for its future material needs.
Therefore: a rational
animal is endowed by nature with the right to
possess permanent private property.
Major: Nature does nothing in vain, hence if a creature cannot live without material things and must get those by its own planning, it has a right to get them and keep them for use.Minor: Other animals live by instinct, but a rational animal lives by deliberate planning for the future.
Proof of Minor: This is the definition of man established by the science of psychology.
- Objection: The state can provide man with his material needs.
- Answer: Man's duty and right to provide for himself is prior to the state, and cannot be taken away by the state.
- Another objection: Man may have a right to what he produces, but not the land.
- Answer: Since man has a right to what he produces from the land, he must also have a
right to keep the land in order to produce from it.
- In the above demonstration the student will note that Leo XIII argues from the following principles:
- 1. Man is a rational animal. This is a definition which comes from the theoretical science of psychology.
- 2. Man has a moral right to those things which are necessary for him to live a good human life. This is a basic principle of ethics.
- In the above demonstration the student will note that Leo XIII argues from the following principles:
3. Man's need for permanent possession of material things, and his ability to acquire them by labor, is prior to the state. This is a basic principle of politics.
Leo XIII's proof is certainly scientific and leads to a necessary conclusion. However, as he himself indicates when he points out that the laws of individual society limit this right, this general conclusion has to be applied to the particular circumstances of each society. It is not wrong for the state to take over ownership of certain kinds of property if this is necessary for the common good, as long as it does not violate the basic right of the individual to own what he needs. The conclusions of the social sciences usually admit of such modifications in practice according to differing circumstances, except in cases where what is involved is intrinsically evil and contrary to nature, in which case the action is always wrong, whatever the circumstances.
ST.THOMAS AQUINAS AND THE MATERNITY OF OUR LADY
The following is from the Summa Theologiae, Part III, Question 35, Article 4.* [*Reprinted from the Summa Theologica, Benziger Brothers, Inc., publishers and copyright owners.]
Whether the Blessed Virgin Should Be Called the Mother of God?
We proceed thus to the fourth article:
Objection 1. It would seem that the Blessed Virgin should not be called the Mother of God. For in the divine mysteries we should not make any assertion that is not taken from Holy Scripture. But we read nowhere in Holy Scripture that she is the mother or parent of God, but that she is the mother of Christ or of the Child, as may be seen in Matthew 1:18. Therefore we should not say that the Blessed Virgin is the Mother of God.
Objection 2: Further, Christ is called God in respect of his divine nature. But the divine nature did not first originate from the Virgin. Therefore the Blessed Virgin should not be called the Mother of God.
Objection 3: Moreover, the word God is predicated in common of Father, Son, and Holy Ghost. If, therefore, the Blessed Virgin is Mother of God, it seems to follow that she was the Mother of Father, Son, and Holy Ghost, which cannot be allowed. Therefore the Blessed Virgin should not be called Mother of God.
On the contrary, in the chapters of Cyril, approved in the Council of Ephesus, he read: "If anyone confess not that Emmanuel is truly God, and that for this reason the Holy Virgin is the Mother of God, since she begot of her flesh the Word of God made flesh, let him be anathema."
I answer that, as stated above (Question 16, Article 1), every word that signifies a nature in the concrete can stand for any hypostasis** [** Technical term used by the Greek Fathers equivalent to substance. ] of that nature. Now, since the union of the Incarnation took place in the hypostasis as above stated (Question 2, Article 3), it is manifest that this word God can stand for the hypostasis, having a human nature and a divine nature. Therefore, whatever belongs to the divine and to the human nature can be attributed to that Person: both when a word is employed to stand for it signifying the divine nature, and when a word is used signifying the human nature. Now conception and birth are attributed to the person and hypostasis in respect of that nature in which it is conceived and born. Since, therefore, the human nature was taken by the divine Person in the very beginning of the conception, as stated above (Question 33, Article 3), it follows that it can truly be said that God was conceived and born of the Virgin. Now from this is a woman called a man's mother, that she conceived him and gave birth to him. Therefore the Blessed Virgin is truly called the Mother of God. For the only way in which it could be denied that the Blessed Virgin is the Mother of God would be either if the humanity were first subject to conception and birth, before this man were the Son of God, as Photinus said; or if the humanity were not assumed unto unity of the Person or hypostasis of the Word of God, as Nestorius maintained. But both of these are erroneous. Therefore it is heretical to deny that the Blessed Virgin is the Mother of God.
Reply to Objection 1. This was the argument of Nestorius, and it is solved by saying that, although we do not find it said expressly in Scripture that the Blessed Virgin is the Mother of God, yet we do find it expressly said in Scripture that "Jesus Christ is true God" (as
may be seen, I John, 5:20) and that the Blessed Virgin is the Mother of Jesus Christ, which is clearly expressed in Matthew 1:18. Therefore, from the words of Scripture it follows of necessity that she is the Mother of God.
Again it: is written (Romans 9:5) that Christ is of the Jews "according to the flesh, who is over all things, God blessed forever." But he is not of the Jews except through the Blessed Virgin. Therefore he who is "above all things, God blessed forever" is truly born of the Blessed Virgin as of His mother.
Reply to Objection 2: This was an argument of Nestorius. But Cyril, in a letter against Nestorius, answers it thus: "Just as when a man's soul is born with its body, they are considered as one being: and if anyone wish to say that the mother of the flesh is not the mother of the soul, he says too much. Something like this may be perceived in the generation of Christ. For the Word of God was born of the substance of God the Father: but because be took flesh, we must of necessity confess that in the flesh he was born of a woman." Consequently, we must say that the Blessed Virgin is called the Mother of God, not as though she were the Mother of the Godhead, but because she is the mother, according to his human nature, of the Person who has both the divine and the human nature.
Reply to Objection 3: Although the name God is common to the three Persons, yet sometimes it stands for the Person of the Father alone, sometimes only for the Person of the Son or of the Holy Ghost, as was stated above (Question 16, Article 1). So that when we say, "The Blessed Virgin is the Mother of God," this word God stands only for the Incarnate Person of the Son.
In the body of this article St. Thomas states his proof positively and negatively:
A. Positive demonstration:
The mother of a divine
Person according to his
human nature is rightly called the Mother of God,
And: Mary is the mother of a divine Person
according to his human nature.
Therefore: Mary is rightly called the Mother of God.
Major: Because a name is given with respect to what is personal (proved in Question 16, Article 1).Minor: Mary is the Mother of Christ, who is a divine Person having a divine nature from all eternity and a human nature taken from Mary (Question 33, Article 3).
Notice that the major here rests on a philosophical truth (namely, the right way to give names) while the minor is a revealed article of faith. This is typical of theological reasoning, that frequently one premise is taken from faith and one from reason, although sometimes both are taken from faith.
B. Negative demonstration:
If one holds that Mary should not be called the Mother of God, this must logically be because he holds either that:
- 1. Christ only became the son of God after he was born of Mary.
- 2. Or that in him there was not one single divine Person, but a divine and a human person.
- But: both of these positions have been condemned by the Councils as heresy.
- Therefore: to deny that Mary is to be called the Mother of God is equivalent to heresy.
- 2. Or that in him there was not one single divine Person, but a divine and a human person.
The objections and their answers:
We can briefly formulate these objections and the distinctions by which St. Thomas answers them as follows:
1. A woman who is not
given this title in Holy
Scriptures is wrongly called the Mother of God.
And: Mary is a woman who is not given this
title in Holy Scriptures.
Therefore: Mary is wrongly called the Mother of God.
Answer: distinguish the
major: who is not given this title implicitly, I concede.
who is not given it explicitly, I deny.
Contradistinguish the minor:
Deny that the conclusion follows.
2. A woman who is not the origin
of Christ's divine nature is wrongly called the Mother of God.
And: Mary is a woman who is not the origin
of Christ's divine nature.
Therefore: Mary is wrongly called the Mother of God.
Answer: distinguish the major: "wrongly called the Mother of God
as if she gave him his divine nature,"
I concede.
"wrongly called the Mother of God
as the Mother of a divine Person
with regard to his human nature,"
I deny.
Distinguish the minor:
And distinguish the conclusion.
3. One who is not the Mother
of the Blessed Trinity is wrongly called the Mother of God.
And: Mary is not the Mother
of the Blessed Trinity.
Therefore: Mary is wrongly called the Mother of God.
Answer: distinguish the major. "Mother of God" if "God is used to
mean the Three Persons in common, I concede.
But if "God" is used to signify the Second Person, I deny.
Distinguish the minor.
Distinguish the conclusion.