In the last chapter we indicated that, while mathematical calculation was developed in a practical way by the people of Mesopotamia and Egypt, and carried still further by the Hindus and Chinese, it was the Greeks who made it a theoretical study. They transformed it into a true science, rigorously logical in structure, and a model for all other sciences.
It was these same scientifically minded Greeks who first arrived at a perfect conception of the fine arts. The art of Mesopotamia was strong and grandiose, but without grace or subtlety. The art of Egypt was subtle and mysterious, but strangely static and without inner thought or feeling. Only in the art of Greece is there achieved a living balance of all the elements of beauty. Their art was classical (from Latin classicus,meaning "first class"), and became a standard for all later art. Not, indeed, that art of later ages need confine itself to copying the style and subject-matter of Greek art, as some people have thought but that we can learn from Greek literature, sculpture, and architecture a true conception of the elements that go into a work of art and of the harmony with which they should be united.
Today we are inclined to think of science and art as unrelated fields. The artist seems to be all imagination and emotion, living in a subjective world of free fancy. The scientist seems to be all facts and abstract theories, living in the objective world of experiment and measurement. Yet the Greeks excelled both in art and science. In order to learn something of this lesson from the Greeks in this chapter we are going to try to get clearer notions of two questions:
1. Why is mathematics a science?
2. Why is beauty mathematical?
Plato (429-347 B.C.) had learned to love the pursuit of scientific knowledge from the great Socrates. When Socrates was put to death by the Athenians as a "corrupter of youth" because lie had aroused this love of truth in the young men of the city, Plato left Athens and journeyed far and wide in search of a teacher. In Cyrene, in Africa, he studied mathematics with an important teacher named Theodorus. In Italy he met two famous men, Archytas of Tarentum and Timaeus of Locri, who belonged to the ancient tradition of the Pythagoreans and who also were fascinated by mathematics. On returning to Athens, Plato opened his school, the Academy, and engraved over its portal the famous inscription:
Around him lie gathered a number of pupils, some of them especially brilliant in mathematics. We know from Plato's work, The Republic, Book VII, that arithmetic, geometry, astronomy were considered by him to be the indispensable foundations for the study of philosophy. Although he himself was occupied principally with philosophy, be encouraged his followers to develop these preliminary branches of science. Menaechmus, Dinostratus, Athenaeus, Helicon, and especially Eudoxs made very important mathematical discoveries. Their names today seem strange to us, and yet the very mathematical theorems which they first worked out are still taught in our study of mathematics.
Among these pupils of Plato, Aristotle bad the most universal mind. He did not give special attention to mathematics because it was by then the best developed of the sciences, and he was anxious to extend the scientific method to wider fields, especially to physics, chemistry, and biology. But lie did make a fundamental contribution to mathematics: lie explained and defended the axiomatic or logical method in mathematics without which it cannot be a true science.
It was not until about 300 B.C. (some twenty years after Aristotle's death) that the first great mathematical work employing this axiomatic method was written in Egypt, in the city of Alexandria where the followers of Plato and Aristotle had founded new schools. This was the book called the Elements, the work of an obscure teacher named Euclid.
We know little about Euclid except this book and a few lesser ones, but a story is told about him which well illustrates his attitude. A pupil who had just learned the first theorem in geometry turned to his teacher and asked: "What do I get by learning such things?" Euclid did not answer, but calling for a slave said to him: "Give this fellow threepence [a slave's wages] since he must be paid for what he learns." For Euclid, mathematics is a theoretical subject to be learned because it is true and not because it is useful. He called his book the Elements because it contains the foundations of both branches of mathematics, arithmetic and geometry.
This book has been more widely used than any other book we know of, except the Bible. Not only was it a basic textbook for Greek, Roman, and medieval schoolboys, but also for the students of the Mohammedan countries. It was used in schools until about fifty years ago, when it began to be replaced by easier books. Is this the reason that we find such a deficiency in mathematics among students today? Can it be that modern youth is incapable of thinking as clearly as young people did in past times? We are accustomed to think of our age as much more scientific than days of old, and yet we find it too hard to master the book which has been the foundation of the whole history of science.
Let us take a look at this great book.
Aristotle had stated the scientific ideal as follows:
We suppose that we possess perfect scientific knowledge of a subject, as contrasted to knowing it in the haphazard way that a sophist knows it, when we think that we know the cause on which the fact depends as the cause of that fact and no other, and further, that the fact could not be other than it is. (Posterior Analytics, 1, c. 2, 71b 8.)Aristotle knew perfectly well that such a high ideal of knowledge is not easy to obtain and is rarely actually achieved, but we must measure our knowledge by the most perfect type of knowledge possible. Euclid hoped to achieve such knowledge at least in the relatively easy field of mathematics.
You will notice that the difference between science and opinion does not consist in the fact that science is obtained by experiments or the use of some complicated instrument (like a microscope or Geiger counter), while opinion is not. Nor is the difference that science uses measurement, and opinion does not. Nor is it that science is objective, opinion subjective; nor that science is certain, opinion probable. We can have opinions that are certain, objective, acquired by measurement, instruments, and experiment -- and they still remain only opinions. We can have science, on the other band, which involves no instruments, nor experiments, nor measurements (although it must be certain and objective). What makes science to be true science is that it gives us the proper reason for a certainly established fact. Until we have discovered such a proper reason we do not have perfect science, and are still at the level of opinion.
Consequently, mathematicians before Euclid were mainly at the level of opinion, because they had not carefully built tip the science of mathematics in such a logical and orderly way that they could see the proper reasons for their conclusions.
In order to correct this, Euclid kept before his mind the four questions which Aristotle had outlined as the basic questions that must be asked in every science:
- 1. Does the thing we are trying to study really exist? For example: Is there really such a thing as a circle?
Until we can answer this question there is no use going any further. It is impossible to have scientific knowledge of something that does not exist, or at least which has not existed at some time. "Scientific" guesses about the future are opinions, not science.
- 2. What is its definition? For example: What is a circle?
It might seem that we must first have the definition of a circle before we can even ask if it exists. This is true of the nominal definition (see page 129), which tells us the usage of the word "circle." But the real definition cannot be given until we have answered Question 1, since there is no way to find out what a thing is, unless it is (exists).
- 3. What are its properties? For example: Can a circle be drawn inside a square so as to touch all sides of the square?
Here, also, we first need a nominal definition of the property. In the case of a property this is sufficient, since in answering the next question we will also settle whether the property exists or not.
- 4. What is the proper reason that this thing (real definition required) has this property (nominal definition)? For example: Why can a circle be drawn inside a square?
When we know the answer to Question 4, at the same time we know the answer to Question 3. When we know the proper reason that a property is necessarily connected with its subject, we know that property must exist.
In setting up his Elements, Euclid tries to answer these questions in the correct order.
If we open the Elements we find that it is divided into thirteen books as follows:
| Plane Geometry: | Book I: Lines, triangles, parallelograms.
(The next to the last theorem is the famous Pythagorean theorem.) Book II: Areas of triangles and parallelograms. Book III: Circles. Book IV: Figures circumscribing or circumscribed by circles. |
| Proportion: | Book V: Ratio and proportion.
Book VI: Similar figures and proportional lines. |
| Arithmetic: | Book VII: Numbers and their properties.
Book VIII: Ratio and proportion in numbers. Book IX. Ratio and proportion in numbers, continued. |
| Incommensurables: | Book X: Commensurable and incommensurable magnitudes. |
| Solid Geometry: | Book XI: Intersections of planes, parallelipipeds.
Book XII: Pyramids, cylinders, cones, spheres. Book XIII: The five regular Pythagorean solids. |
At the beginning of the first book there is a long list of definitions (23 of them), and at the beginning of most of the subsequent books there are further definitions. These definitions are nominal ones, merely telling us the meaning of the words Euclid is going to use. A study of these definitions is very valuable in clarifying our thinking, and we will discover that some of Euclid's definitions are not perfect. For example, his first definition is: "A point is that which has no part." It would be better to define a point as "that which is indivisible but which has position," as Aristotle defined it. Why is Aristotle's definition more exact?
Next Euclid had to answer the first of the scientific questions: Do these things which have been nominally defined really exist? He does this by stating the following postulates:
- A straight line may be drawn from any point to any point.
- A straight line may be extended in a straight line.
- A circle can be drawn around any point as center and with any radius.
- All right angles are equal to one another.
- If a straight line falling on two straight lines makes the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which the angles are less than the two right angles.
Actually, Aristotle had already indicated that it would be sufficient to postulate only two things:
- The existence of points.
- The existence of lines.
These are both needed because a magnitude (continuous quantity, see page 316) can only be defined in terms of the simplest continuous quantity, namely, a line, while lines must be differentiated by their position (given by points). Planes, solids, and any kind of figure in them can be constructed by means of lines and points, as Euclid actually proceeds to do.
How do we know that these postulates are true? Euclid does not attempt to prove them, because then they would not be first principles. On the other band, be does not merely assume them. He takes them as immediately evident to us from our experience of physical quantity, or rather from our images of physical quantity as derived from such experience.
These postulates are the proper principles belonging to the science of magnitude. Indeed, they amount to a definition of the subject of that science, since when we define a line and a point we really define magnitude (continuous quantity). In addition to these, we also make use of common principles or axioms which the student must know even before he begins to study this science and without which lie would not be able to understand the teacher. There are many such axioms (see, for example, pp. 354 f.), but the Elements gives only five, and some authorities believe that the last two of these were added by writers after Euclid:
- Things which are equal to the same thing are also equal to each other.
- If equals be added to equals, the wholes are equal.
- If equals be subtracted from equals, the remainders are equal.
- Things which coincide with one another are equal to one another.
- The whole is greater than the part.
These are axioms and not postulates, since they apply (but in an analogous sense) both to numbers (discrete quantity) and to things that are not quantities at all. For example, a happy life (which is not a quantity) is greater (better) than pleasure (which is a part of a happy life).
Euclid actually used other axioms, such as the principle of contradiction (see page 575), but these are the ones most directly needed in his proofs.
Thus Euclid began his science of magnitude with a secure foundation, as Aristotle had required. Every science must rest on first principles which are immediately evident from experience. These first principles are:
- Axioms, or common principles, required even before we begin to study the subject.
- Postulates (hypotheses, as Aristotle calls them) which give us the real definition of the subject to be studied by asserting its existence.
- Definitions (theses in Aristotle's terminology) of the terms (nominal definitions) or properties which are to be demonstrated.
- Middle terms which can connect the subject with its properties.
Given these principles we can form a demonstrative syllogism (see page 75) as follows:
Every M (a middle term
which gives a nominal
definition of the Property) is P (name of the property to be proved)
And: every S (name of the
subject to be studied) is M (middle term which gives a real
definition of the subject)
Therefore: every S (subject) is P (property).
In this syllogism we will notice that the middle term is identical in both premises (otherwise it would not be a middle term), but that it has two different functions. In the major premise it is only a nominal definition of the property, while in the minor premise it is the real definition of the subject. How can this be? A property is an accident (see page 44), and to define an accident we must include the subject in which it exists. Hence the nominal definition of a property includes a reference to its subject as the cause of its existence. For example, if I ask, "What is a smile?" you must answer with the nominal definition: "The word 'smile' means a curving of a man's lips." In this definition you have mentioned the subject in which the smile exists, namely, "a man's lips."
Thus the middle term of a demonstration is: 1) The term used in both premises (and not in the conclusion) of the syllogism; and 2) at the same time a real definition of the subject, and a nominal definition of the property as it exists in the subject which is the cause of its being. The smile exists in a man's lips, and it is caused to exist by the man, who exists in himself.
Euclid's first demonstration is the following proposition or theorem: On a given finite straight line to construct an equilateral triangle.
Steps of Proof Reason
1. Let AB be a given finite straight
line. Postulate 1.
2. With point A as center and radius
AB, let a circle be described; again,
with point B as center, and radius
BA, let another circle be described. Postulate 3.
3. From the point C, in which the
circles cut one another*, to the
points A and B, let the straight
lines CA, and CB be drawn. Postulate 1.
[* It is well known that it is a fault in this proof that Euclid does
not prove that the circles will cut each other in a point, although
this can be proved. See The Thirteen Books of Euclid's Elements,
translated with introduction and commentary by Sir Thomas L. Heath
(second edition, unabridged; Dover: 1956), Vol. I, pp. 242 ff.]
4. But: AC is equal to AB, and BC
is equal to BA Definition of a circle, namely,
that every point of its
circumference is equidistant
from the center, plus
postulate 3 (that there exist
such circles of any radius
around any point).
5. And: CA is equal to AB CA and AC is same line (step 4).
6. Therefore: each of the straight
lines CA and CB is equal to
AB Summary of foregoing
(steps 4 and 5).
7. And: things which are equal to
the same thing are equal to
one another. Axiom 1.
8. Therefore: the three straight lines
CA, AB, and BC are equal
to one another. Step 7.
9. Therefore: the triangle ABC is
equilateral, and it has been
constructed on the given
finite straight line AB. This
was what the proposition re-
quired us to do. Step 8.
To put this proof into strict syllogistic form, it is easiest to work backwards, beginning with the ultimate conclusion (see page 75). This gives us a subject (minor term) and a predicate (major term) which can be arranged in a skeleton syllogism, thus:
Conclusion: S (minor term) P (major term)
The triangle ABC on a finite
straight line AB is an equilateral triangle.
Minor premise:
The triangle ABC on a finite
straight line AB is M (middle term)
Major premise: M (middle term) is an equilateral triangle.
We then have to locate the middle term, which Euclid shows us in his Step 8, namely: three straight lines CA, AB, BC equal to one another. By placing this in both premises in proper position, we have a complete syllogism. It is still necessary, however, to prove these premises; by treating each as a new conclusion to be proved, we continue to work backward until we arrive at nothing but axioms or postulates or definitions. Thus we have the following:
1. A closed plane figure formed
by three straight lines CA,
AB, BC equal to one another is an equilateral triangle.
2. And: the triangle ABC on a
finite straight line AB is a closed plane figure formed
by three straight lines CA,
AB, BC equal to one another.
Therefore: the triangle ABC on
a finite straight line AB is an equilateral triangle.
Proof of 1: Definition: this is the nominal definition of an equilateral
triangle.(Euclid's definition 20.)
Proof of 2:
3. A triangle formed by two
lines CA and CB equal to
its third side AB is a closed plane figure formed by three
straight lines CA, AB, BC equal to one
another.
4. And: Triangle ABC on a
finite straight line AB is a triangle formed by
two lines CA and CB
equal to its third side AB
2. Therefore: triangle ABC
on a finite straight line AB is a closed plane figure formed by three
straight lines CA, AB, BC equal
to one another.
Proof of 3: Axiom 1: Things equal to same thing are equal to each other.
Proof of 4:
5. A triangle whose one side
AB is the common radius
of two circles, and whose
other two sides CA and
CB are radii of same two
circles is a triangle formed by
two lines CA and CB
equal to its third side
AB.
6. Triangle ABC on a finite
straight line AB is a triangle whose one
side AB is the common
radius of two circles,
and whose other two
sides CA and CB are
radii of the same two
circles.
4. Therefore: Triangle ABC
on a finite straight line AB is a triangle formed by
two lines CA and CB
equal to its third side
AB.
Proof of 5: Postulate 3.
Proof of 6: The lines AB, CA, and CB can be drawn -- Postulate 1.
The two circles can be drawn -- Postulate 3. That they
have a common point C is not proved, which is a defect
(see note on page 334).
Every theorem in Euclid can be put into this strict syllogistic form.* A student ought to assure himself of this by working out several of the demonstrations, after which the abbreviated method of Euclid himself should be followed. In this method the steps (conclusions) are stated with their respective reasons (middle terms), but without the explicit statement of both premises. The reason that it is important to be sure that these proofs can be stated syllogistically is that only then are we certain that the proof is logically rigorous. If an argument cannot be reduced to the syllogism, the simplest of all forms of reasoning, it cannot be proved that it is logically valid (see page 568 ff.).
[* The proof just given is a construction theorem and does not constitute the clearest example of demonstrating a property of a subject. Rather it demonstrates the form (equilateral) from its parts (three straight lines), which are like a material cause. In such demonstration the parts are treated as the subject, and their form is treated as a property. This is common in construction theorems, which aim at establishing the real definition. More typical would be Theorem 5 of this First Book of the Elements, in which it is proved that every isosceles triangle (subject) has the base angles equal (property).]
According to Aristotle, a science is well ordered when it begins with the evident and indemonstrable axioms, postulates, and definitions, and proceeds to problems and theorems arranged in the following way:
- 1. We should first prove the properties that belong to the whole subject. For
example, the properties common to all triangles should be proved before we
discuss the properties of equilateral or scalene triangles.
- 2. We should then divide (classify) the subject into its various species or genera and prove the theorems, giving the properties of each species. For example, we should divide triangle into equilateral, isosceles, and scalene, and then prove the properties belonging to each.
- 3. We should then subdivide and continue until we get to the ultimate species which are divided only into like individuals. Thus triangle is completely divided into the three species just given, but polygon would be first divided into regular and irregular, and regular would be subdivided into square, pentagon, hexagon, etc.
- 2. We should then divide (classify) the subject into its various species or genera and prove the theorems, giving the properties of each species. For example, we should divide triangle into equilateral, isosceles, and scalene, and then prove the properties belonging to each.
The reason for this order is to avoid repetition (since what is proved of the genus need not be repeated for each species) but also, and more importantly, in order to discover gradually the properties of things. If we first proved that an equilateral triangle has its interior angles equal to the sum of two angles (180), then we would have to prove it again for all other types of triangles, until at last we discovered that it is not a property of this or that kind of triangle but of all triangles. On the other hand, if we have proved that this is a property of all triangles, then we can use this as a premise in proving some property which an equilateral triangle alone has. This orderly procedure corresponds to the nature of our minds, which most clearly perceive what is general and simple, and which come to a knowledge of details only step by step.
If we look at the outline of the Elements on page 330, we will see that, in general, Euclid has followed this order. He begins with the geometry of lines (not very fully treated) and continues with plane geometry (first four books), working up from triangles to parallelograms, then to circles, and finally to combinations of circles and other figures. Thus he is moving from the simpler and more general elements to the more complex. Books V to X deal with problems of arithmetic and of the application of arithmetic to geometry; we will discuss them in Chapter III (see below, page 353). The last three books, XI to XIII, deal with solid geometry and again build up from what is simpler and more general to what is more complex.
Euclid's order taken as a whole is synthetic (from the Greek for put together"), that is, he begins with simple things and then puts them together into more complex wholes. Thus he begins with the simplest truths (definitions, postulates, axioms) and works in the direction of more and more complicated theorems. He also works from lines to planes to solids, and from simple figures to complex figures. On the other band, some of his proofs are analytic (from the Greek for "take apart"), that is, they begin with the conclusion and work backward to the simple principles on which it is based. The syllogistic arrangement which we give above (pp. 335 f.) is analytic, since we began with the conclusion and worked backward to the premises.* The analytic method is really more fundamental, since even when we proceed synthetically we must always keep connecting each new conclusion with the axioms and postulates.
Euclid uses both synthetic and analytic proofs. An interesting type of analytic proof is the reduction to absurdity (reductio ad absurdum), also called proof through impossibility (per impossible). In such a proof we assume that the contradictory of what we wish to prove is true, and then by argument we deduce an obviously false conclusion from this assumption (see page 143). Because the contradictory of a false statement must be true (see page 138), we are then sure that the original theorem is true.
[* The terms "analytic" and "synthetic" are used in still another sense to refer to propositions in which the truth is evident from the meaning of the terms (analytic) or only as a matter of fact (synthetic).]
THE BEAUTIFUL FITS THE KNOWER
A thing is beautiful when it pleases us just to look at it, hear it, or know it. We are pleased by well-cooked, well-flavored food, because it fits our appetite for food. We are pleased by a comfortable bed, because it fits our need for rest. We are pleased by a paycheck, because it fits our need for purchasing power. We also have an appetite or need for knowledge and experience. We human beings are creatures full of curiosity, hungry for knowledge, although in some this appetite has grown dull because of laziness or discouragement. Therefore, when we meet an object which fits our need for knowledge, we are filled with pleasure.
Such an object which is adapted or fitted for knowledge, as food is cooked and savored for eating, is a beautiful object. It fills our eyes, or ears, or mind with vivid truth. Thus whatever is beautiful must be true, but not everything which is true is beautiful; it may be a truth which is not fitted to our minds, which is dim, obscure, confused, rather than vivid and pleasing. just as tasty food is usually also nourishing, but not all nourishing food is tasty, so, even more truly, beautiful things are true, but truth may not appear beautiful to us, because it is not fitted to our capacity. It follows, then, that the chief thing in beauty is clarity (vividness, brilliancy, splendor, charm).
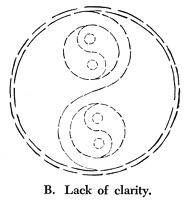
The clearest and simplest example of something beautiful is a pattern or design, like Design A on this page. Why is it beautiful? St. Thomas tells us that beauty consists formally in clarity, and materially in proportion and integrity.
 |
 |
 |
 |
Design A has more clarity than B, because the contrast in color between the black and white parts of the design makes the pattern clear. If it were also in bright hue (for example, blue and yellow), it would be still clearer and more beautiful. Thus clarity makes the design stand out, so that it strikes our eye. This is simply another way of saying that it is fitted to the appetite of our eye for seeing. When we look at Design B it appears confused, and the eye finds it unpleasant. But Design A strikes the eye at once as clear and definite, and hence is pleasant.
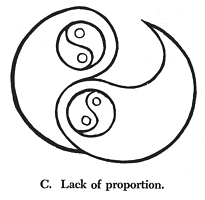
This clarity, however, must be the clearness of a pattern. And what is a pattern or design? It is an arrangement or order of parts to form a whole. Thus C has the same parts as A and B, but they are not in any order. Order is defined as a multitude related to one. An army is ordered because it is made up of many soldiers all related to one general; an orchestra is ordered because there are many players all related to one conductor. Hence a design is a multitude of parts, all of which are related to some one part (in this case to the center).
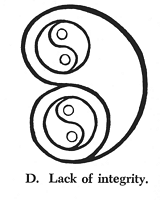
Often this is expressed by saying that beauty is "unity in variety." St. Thomas expresses it more accurately by saying that it must have integrity and proportion. "Proportion" means that every part has a definite relation to the chief part and thus to the whole. "Integrity" means that all the parts needed to establish this relation are present. C lacks proportion because one of the parts is unrelated to the center. D lacks integrity because a part needed to complete this relation is lacking. Thus a good design must have enough parts (variety), i.e., integrity, and all of these parts must be properly arranged (proportion or unity), and this arrangement must be fitted to the knower so that he is able to grasp it vividly (clarity).
In music, in a similar way, there is a definite pattern of sounds. The basic pattern in music is what we call the scale. The range of sounds from very low to very high is continuous, as we hear in a siren, or when the violinist slides his finger along a vibrating string. If all these possible sounds were to be used in music it would be difficult both for the player and the audience to follow a pattern. Hence from this continuum of sounds we select certain tones bearing definite relations to each other, which we call the scale. Between any tone of the scale and any other tone there is some simple relation based on the relation between the number of vibrations required to produce each tone. The most important tones of the scale have the simplest relations to each other, as will be seen in the diagram (page 349). In writing a melody the composer selects tones of the scale in such a way that the most important tones of the scale form the skeleton of his melody, and the less important tones fill in this skeleton. When we hear such a melody it has integrity because all the important tones of the scale are used. It has proportion because the important tones are in the important positions, so that we hear them as having definite relations. Finally, the melody has clarity because the composer emphasizes these relations. He emphasizes them by giving them the longest tones or accented tones (rhythm), by making them louder, by repeating them, by reinforcing them by harmony, or by giving them the most brilliant quality (by using the right quality of voice or the right instrument). In this way the proportions or relations in the melody stand out with clarity and are beautiful.
From this we see that, in producing a beautiful object, pattern or design is extremely important. This does not mean, of course, that beauty (integrity, proportion, clarity) is found only in such patterns. If we take a pure color or tone as seen or beard by our external senses, our eyes or ears, it may be called beautiful too. Its integrity consists in the fact that the color fills a considerable surface, or the tone endures for a sufficient time. Its proportion consists in the fact that the color or tone is pure, uniform. Its clarity consists in the fact that the color is brilliant, or the tone brilliant and sufficiently loud. Here integrity, proportion, clarity are analogous to those found in a pattern, and the beauty is of a different sort.
Similarly, in our intelligence there can also be beauty, for example, in the clear explanation of a mathematical proof or a proof in Christian doctrine. Here the integrity consists in the completeness of the explanation, the proportion in the way in which every part of the proof is perfectly fitted together, and the clarity in the way that the conclusion and the proper reason for it (the principles) stand out distinctly, so that we are freed of all confusion. Again, this beauty is analogous to the beauty of a pattern, but not quite the same.
Which of these three kinds of beauty -- sensible beauty (color, tone), imaginative beauty (designs perceived by our internal senses), or intellectual beauty (abstract truth clearly understood)-is the most perfect? To answer this, we must realize that, in itself, the deepest, truest beauty is intellectual beauty, since only our intellects can penetrate the very nature and essence of reality. Furthermore, it is only the intellect that can know relations. Since beauty is a kind of relation (the fit of the object to the knower), only our intellect understands what beauty is. When we see a beautiful color, our eye is pleased, but only the intellect sees that it is precisely the beauty of the color which is so pleasing. Hence animals, who have no intellect, do not really appreciate beauty as such. For the bee the beauty of the flower is only a signal that honey is to be found there.
Nevertheless, for us human beings intellectual beauty is not completely satisfying. If we were angels such beauty would be so perfect that it would satisfy us, but we have very weak intelligences that can know perfectly only by using our senses. Consequently, when we think of purely abstract truth it seems cold and dead; it does not wholly fit us, unless we can make it concrete somehow by imagining it. The result is that when we think of a man as a "rational animal," our knowledge seems remote and lacking in beauty. When we think of a man with a clear image of a perfect man to illustrate the abstract idea, then it becomes much more satisfying. That is why we like illustrations in a book. Such pictures in our imagination are the kind of patterns we have been speaking of.
On the other hand, a pure pattern without quality, color, or sound also seems cold and diagrammatic. To make a design perfectly beautiful we want it colored and exhibited in a bright light. We want a musical score actually performed and in a sufficiently loud tone. While, therefore, intellectual beauty is most perfect in itself, for us human beings the most perfect beauty is intellectual truth embodied in a visible and audible pattern. God in himself is most beautiful, but his beauty appeared to us best when he became a man and dwelt amongst us, where we could see and hear him.
Thus perfect beauty for us is intellectual, but intellectual truth exemplified in something concrete and visible. If we compare the three types of beauty we get the following scheme:
- 1. Intellectual beauty is most beautiful in itself, but less fitted to us.
- 2. Sensible beauty (external senses) is less beautiful in itself, but most fitted to us.
- 3. Imaginative beauty is a mean between these. On the one hand, it is sensible, we can picture it; yet in a way it is abstract, a pure design.
- 2. Sensible beauty (external senses) is less beautiful in itself, but most fitted to us.
We see, then, that the most perfect beauty requires all three together, but of the three it is imaginative beauty which is most truly beauty for us, since without it the others would not be beautiful. Unless external beauty is somewhat refined by our internal senses, we can never understand its beauty with our intellect; and unless intellectual beauty were made concrete, at least in the imagination, it would not be beautiful for us. Thus it is in the designs or patterns in our internal senses that beauty is found in the plainest way. The other kinds of beauty are understood as analogous to it.
Now a design or pattern in the imagination is something quantitative. If we thinkof a pattern of color or tone, and then remove the color and tone, we will still have a pattern. it will be a unity made up of parts, one outside the other, and that is exactly what we mean by a quantity. This is because quantity is the first of all the accidents of a thing, and hence we can remove the other accidents (abstract from them) without taking away the quantity. If we took quantity away too, we would have only substance, and we cannot imagine, but only know with our intellect, a substance which has no quantity (a spiritual substance). If the pattern we imagine still has figure, then it will still have a minimum of quantity, since figure is the quality limiting a quantity. In a pattern (see p. 340) we still have a magnitude with a figure (circles, curves). But if we take this away, then we have number, and in music we have patterns whose parts are related to each other like numbers. The scale can thus be imagined as a series of ratios.
From these facts we can see why mathematics, which deals with quantities, magnitudes, and numbers, is so very important in understanding beauty. It is just at this point that the most obvious kind of beauty is found, in geometrical patterns and in numerical relations.
It will be astonishing to some people to think of mathematics being beautiful, to hear that artists are concerned with mathematics. Of course, mathematics is not beautiful to those who do not understand it, because what is obscure is not clear. But to those who study it, mathematics is the clearest of all subjects. It is also true that many artists do not know mathematics, and work out their designs or compositions by the mere feeling that the design "looks right." Nevertheless, if we study the history of art and music we will see that all the great new advances in art and music were made possible by artists who studied mathematics and learned from it how to make new and more beautiful patterns. Thus the great achievements in art by the Greeks and by the artists of the Renaissance were due to men like Leonardo da Vinci who studied the use of mathematics in art. Similarly, the advance of music from simple unison singing to harmony was made possible only by mathematical studies. Today modern art is making great use of such mathematical ideas.
Mathematics helps art both materially and formally. Materially it gives to the visual artist all sorts of new figures to use in art, and to the musician new scales, harmonies, and instruments. If we look at Greek art we see that the circle, the cube, the triangle, the rectangle, the cylinder, the pyramid made up almost the whole "vocabulary" Of Greek architecture. But in baroque art, and now very much in modern art, all sorts of new figures are common; shapes like eggs, like guitars, like the forms of the amoeba, parabolas, hyperbolas, saddle-shapes, etc., are used very effectively. These were originated or explained by mathematics. In like manner there has been a steady growth in the musical vocabulary from simple melodies to harmony, and then to various degrees of harmonic complexity. Thus the artist has more variety (integrity) to work with, and understands more complex relations (unity, proportion).
The formal contribution of mathematics to art, however, is in showing how the artist can make his proportions clear, since it is in this that beauty consists. If we compare Greek art at its best with its less developed or later degenerate forms. or with other types of less perfect art, such as that developed by the Babylonians, we see that the reason the Greeks excelled was not because they had different materials to work with (either physical materials, or figures and quantities), but that they knew how to emphasize these designs so as to make them clear as crystal. This was due to the Greek insight into mathematical relations. Similarly, in listening to music we realize that the development of music in the classical period (say from Bach to Mozart) was one of increasing understanding of pure form. In modern art the effort of some of our greatest artists is to take the rich but confused material provided by romanticism and again give to it a clarity of formal structure.
We cannot here go into the details of how mathematics can do this. We can give a simple example, and then show the basic principle on which this theory must be based. If we look at the human body, we see that it is very complicated and that in no two human beings are the proportions the same. An artist, wishing to make a picture of a man and to make it as beautiful as possible, seeks to find in the body some kind of clear order. To do this he can simplify the pattern of the body by thinking of the head as a sphere, the neck as a cylinder, the trunk as two cubes, one for the chest, one for the abdomen, etc. But to find unity in the whole body he looks for a common unit to which all others can be related and by which they are measured, since order means relation to a principle or unit. This unit is called mathematically a modulus. Generally speaking, in the human body the length of the head is such a natural modulus, so that the proportion of the rest of the body can be calculated from it. Here is Leonardo da Vinci's calculus:
The architect Vitruvius states in his work on architecture that the measurements of a man are arranged by Nature thus: -- that is, that four fingers make one palm, and four palms make one foot, six palms make one cubit, four cubits make once a man's height, and four cubits make a pace, and twenty-four palms make a man's height, and these measurements are in his buildings.If you set your legs so far apart as to take a fourteenth part from your height, and you open and raise your arms until you touch the line of the crown of the head with your middle fingers, you must know that the centre of the circle formed by the extremities of the outstretched limbs will be the navel, and the space between the legs will form an equilateral triangle.
The span of a man's outstretched arms is equal to his height.
From the beginning of the hair to the end of the bottom of the chin is the tenth part of a man's height; from the top of the breast to the crown of the head is the sixth of the man; from the top of the breast to where the hair commences is the seventh part of the whole man; from the nipples to the crown of the head is a fourth part of the man. The maximum width of the shoulders is in itself the fourth part of a Man; from the elbow to the tip of the middle finger is the fifth part; from this elbow to the end of the shoulder is the eighth part. The complete hand will be the tenth part. The center of a man is at the crotch. The foot is the seventh part of the man. From the sole of the foot to just below the knee is the fourth part of a man. From below the knee to the crotch is the fourth part of the man.
The parts that find themselves between the chin and the nose and between the places where the hair and the eyebrow start, each of itself compares with that of the ear, and is a third of the face.*
[* The Notebooks of Leonardo Da Vinci, arranged, rendered into English and introduced by Edward MacCurdy (London: Jonathan Cape, 1938) Vol. 1, pp. 225 f.]
The same thing can be applied in architecture, where a building can be fashioned so as to have all its parts related to one modulus or standard unity.
What is the principle behind this? It is the principle of mathematical proportion. In arithmetic we learn that if we compare any two numbers they are said to have a certain ratio (relation) to each other, which we call a "fraction." Thus 1/2, 2/4, 4/8, 25/50 are pairs of numbers having the same ratio to each other, that is the relation of half, while 2/1, 4/2, 8/4, 50/25 have the ratio or relation of double.
All of arithmetic really deals with such numerical relations or ratios; in a musical or visual pattern all the relations are ratios. But if we are to make each relation clear (and this is required for beauty), we must somehow make it as determinate as possible. We must define it. We have already learned in logic that, in order to define something and to make it clear, we compare one thing with another. Hence to define a ratio very exactly we may compare it to another ratio, and such a comparison of one ratio with another is called a proportion (we have already met this notion in studying analogy; see page 50). If we state the ratio 2:4, for example, it might have two meanings: either that 4 is double 2, or that it is the square of 2; but when we write 2:4 :: 3:9, then we determine this relation to mean that of square, and in this way make it clear.* [* Ordinarily such proportions are not written in arithmetic, every proportion being taken in the sense of a fraction, i.e., of simple multiplication.] It is in this way that proportions enable us to specify, clarify, or emphasize ratios or relations. Hence we can understand that when we say a design must have proportion, we mean that it must have similar ratios between each part and some principal part or the whole; it must have order. For example, in a circle divided into four quarters, each quarter has the same ratio to the center and to the whole circle as does each of the other quarters; hence they are in proportion.
A simple proportion must have four terms. Any proportion with more than these is compound and can be divided into a series of simple proportions. It cannot have less than four terms, because it must be a comparison of two relations, and each relation (ratio) must have two terms. However, it is possible to repeat one or two of the terms in a proportion. Thus we can have 2:4 :: 4:8, or a:b :: b:c.
In a proportion, the first and fourth terms are called extremes, the second and third, the means. The various kinds of proportions and the rules of operation which govern them are studied in algebra. Continuous quantities, or magnitudes, lines, and areas, can also be com pared so as to form proportions.
The artist who studies such proportions will be able in his paintings or music to produce wonderful new designs having integrity, proportion, and clarity-and hence beauty.
If we strike a stretched string it will vibrate as a whole, but its parts will also vibrate at the same time; the shorter the part, the more rapid will be its vibration and the higher the tone it emits. All these partial tones blend together to form what sounds to our ear like a single rich tone. By shortening the string with our finger at the proper point, however, we may obtain these various partials. The result will be as follows:
Partial Part of String (Ratio) Piano Tone Scale Note
12th 1/12 G ' ' ' sol
11th 1/11 F ' ' ' fa sharp (too flat)
10th 1/10 E ' ' ' mi
9th 1/9 D ' ' ' re
8th 1/8 C ' ' ' do
7th 1/7 B flat ' ' ti flat (too flat)
6th 1/6 G ' ' sol
5th 1/5 E ' ' mi
4th 1/4 C ' ' do
3rd 1/3 G ' sol
2nd (1st over-
tone) 1/2 C ' do
1st, or funda-
mental 1 (whole string) C do
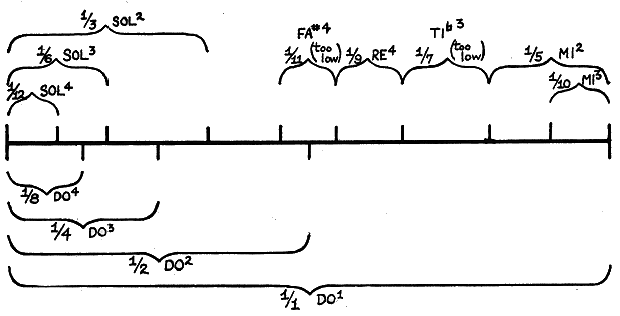
Thus our scale has chosen the tones do, mi, sol because they stand in a simple natural ratio to each other as its most important tones. Re also is an overtone, but fa, ti, la are not. These other tones are chosen by what is called the "circle of fifths" (a major fifth being the interval between do and sol) which gives the following proportion:
We cannot go further because the distance from ti to fa is shorter than the other intervals. The resulting scale, called the major diatonic scale, is as follows:
16/15 half-step do 2/1
9/8 whole-step ti 15/8
10/9 whole-step la 5/3
9/8 whole-step sol 3/2
16/15 half-step fa 4/3
10/9 whole-step mi 5/4
9/8 whole-step re 9/8
do 1
The ratios are between the number of vibrations per second of the tone compared with those for do. In the second column they are ratios of the vibrations of the succeeding note to the previous note, i.e., the ratio of the interval. Note that the whole steps are actually of two sizes, but in practice this is ignored. Such a scale gives the following intervals, which are mainly simple:
Unison: 1:1 Major sixth: 5:3
Octave: 2:1 Minor sixth: 8:5
Fifth: 3:2 Major tone (larger whole step): 9:8
Fourth: 4:3 Minor tone (smaller): 10:9
Major third: 5:4 Semitone: 16:15
Minor third: 6:5
If we determine the frequency ratios of all the intervals in the scale larger than a whole-tone and less than a seventh in the scale, we find that there are 29, of which 23 are
perfect because they can be formed as simple ratios. Four others are quite close to other
intervals that are perfect. Only the tritones are without definite proportion. Thus the
superiority of the just or Ptolemaic scale is apparent because it contains so many
consonances.*
[* See a longer discussion in H. B. Lemon and M. Ference, Jr., Analytical Experimental Physics (Chicago: University of Chicago Press, 1943) p. 464.]
The scale can be constructed by taking the pattern of the most important tones do, mi, sol, which form a chord or major triad (the I Chord). If this is then constructed with sol as the root or bottom tone, we get sol, ti, re (the V Chord). Finally, if we construct a chord so that do is the upper tone, we get fa, la, do (the IV Chord). This gives a complete scale arranged in the following pattern:

It will be noticed that there are intervals of three sizes, but for practical purposes the whole steps are all counted as equal. Thus the scale has the pattern (naming the steps):
Thus harmony is based on the I Chord (do, mi, sol) as the most Perfect (indicating the whole scale), on the V Chord (sol, ti, re) and the IV Chord (fa, la, do) which tend to move or resolve to it, and on any other chords tending to it through the V and IV.
The integrity of the scale, therefore, is due to the fact that it has only those tones required for these three chords. Its proportion comes from the fact that the same pattern (the major triad) is found in each of these chords, but that one of them (the I Chord) is primary, and the other chords are ordered to it. The clarity comes from the fact that I Chord is made up of the strongest overtones, standing in simplest relation to the basic tone (tonic) of the scale, so that we clearly feel these tones as the most concordant (similar or blending) possible.
We may ask, however, why the pattern do, mi, sol is clearly proportioned? It is because it suggests the complete scale made of two proportions:
do:re::mi:fa :: sol:la::ti:do
In this pattern, the two halves of the scale are alike and the alternate tones are concordant with each other, since they suggest this pattern. It is not necessary, however, to play ti, because the first proportion gives us the pattern, and sol indicates that the pattern will be repeated using sol as the base instead of do. It is this principle of proportion which is the proper reason for the concords and discords in the scale.
We might also ask whether some other selection of tones would not be preferable, and we may answer:
- Any number of tones other than a multiple of 4 would not form perfect proportions.
- 4 tones would be too few, because we need to be able to imitate a motion which must have a beginning, middle, and end.
- 12, 24, etc., would be divided into 3 parts, but then they could not form larger proportions having 4 terms.
- Therefore, 16 or 8 tones are best, and 8 is more practical.
- The intervals should not be all the same for the sake of variety (integrity).
- The small intervals should be at the end of ascending motion because the effort increases with rising pitch.
The other possible scales are inferior to the major diatonic scale in the above respects.