MATHEMATICS AS A LIBERAL ART
CHAPTER I
The Science of Numbers
WHY MATHEMATICS IS A LIBERAL ART
In the Old Testament the God-inspired authors gave us a summary of the way in which men of ancient times had come to understand the world about them. In those days men were fascinated by the numbers and measures of things. Even the most primitive of men counted and measured things for practical purposes, using their fingers as their standard, so that even today most systems of counting are based on 10's. In the Old Testament we find the patriarchs counting their sheep, measuring out their plots of land, weighing grain and money. Many people still do not see anything more to numbers and measures than their practical use in keeping accounts or working out engineering problems.
Yet ancient men saw something in measures and numbers which was more important than these practical values. They saw them as a reflection of God's wisdom in making and ordering the world. The wise man says to God the Creator, "You have disposed all things by measure, number, and weight." (Wisd. 11:20). That is why in the poetic account of Creation given in the first chapter of Genesis the inspired writer arranges the works of creation according to 7, the perfect number.
Why did they regard 7 as a perfect number? We are not sure, but it is probably because they had observed that in the heavens, besides the fixed stars, there are seven luminaries that change their position; the Sun, the Moon, Venus, Mercury, Mars, Jupiter, Saturn, and after these they named the days of the week (as we still do, using the Germanic names).
As we read both the Old and New Testament, we are struck with how often numbers are carefully mentioned, and if we study these we will find that many are used as symbols. 1 stands for God as the source of all things. 3 stands for God also as he is the Blessed Trinity and the One who contains in his Unity many perfections. 5 stands for a list of duties or obligations, as in the 5 Books of the Law (Genesis, Exodus, Leviticus, Numbers, Deuteronomy) and 5 books of the Psalms, and 10 Commandments (which include duties to God and neighbor). 7 is the number of perfect time, of a complete week, and a complete cycle of years. 9 is 3² and therefore an emphatic three (as in our Kyrie Eleison). Thus the odd numbers are thought of as indicating perfection, because they are unified and cannot be divided.
The even numbers have a different significance. 2 indicates war or opposition, but it also indicates friendship, love, marriage, and also the confirmation of a testimony by a witness, since at least 2 witnesses are required at law. 4 is the number of the corners of a square, and was thought to symbolize the solid earth, or a solid building. Hence the universe was also thought of as having 4 corners, 4 winds, 4 quarters, 4 elements, and to be presided over by the 4 Cherubim who had faces like a man, an eagle, a bull, and a lion (the four most powerful living things: the eagle among birds, the bull among domestic animals, the lion among wild animals, man above all) with which we are familiar as symbols of the Four Evangelists.
6 was considered the number of evil, because it comes one short of 7 and is like the universe without God (the six days of Creation without the seventh on which God approved his work). Hence St. John the Evangelist in the Apocalypse uses 7 × 7 to stand for the Church and 666 (3 6's) to stand for Antichrist, the evil one who pretends to be God (3). 8 is considered the number of eternity because it is 7 + 1, the eternal day that follows on the week of time. Hence our divine Lord lists 8 beatitudes, and 7 petitions to the Lord's Prayer, because we pray for the coming of his kingdom, but the beatitudes are the rewards of those who will enjoy his kingdom forever. 12 is the number of the Twelve Tribes of Israel and of the Twelve Apostles, because as 3 × 4 it represents a nation (a four-square city) blessed by God (3), and the apostles are the foundation of the New Israel, the New City of the Church. 144,000 which is 122 × 1000 stands for all the elect who will enter heaven, namely, a vast multitude who have belonged to the Church.
The ages of the world are sometimes 7, and sometimes 12 (for the number of hours in the day), and we live at the 11th hour. Finally the number 14 (7 × 2), which is the sum of the letters in the name of David (using the letters as numerals, as the Jews sometimes did), symbolizes the Messias, the descendant and heir of David, so that in the genealogy of our Lord in the Gospel according to St. Matthew the generations from Adam to Christ are listed as 3 × 14.
This symbolism could be superstitious. It becomes so when it is used today in the pseudo-science called numerology, because numbers can be merely accidental things without any meaning at all. But as used in the Scriptures it is a beautiful metaphor to express profound ideas, and a recognition of God's order in the world. We find it not only in the Books of Moses, but especially in the prophecies of Ezechiel and Daniel, in our Lord's own sermons, and in the writings of St. John, climaxing in the wonderful symbols of the Apocalypse.
The love of numerical symbolism found in the Bible reflects the culture of the great archaic civilizations of Mesopotamia and Egypt in the midst of which the Jews dwelt. As the pyramids, towers, and other great buildings of Egypt and Mesopotamia have been uncovered, we have come to read their records kept on stone or clay
tablets, and we begin to see what a great part number and measure played in the lives of the men of these ancient cities.
The proportions, shapes, and arrangements of the buildings show how much men then appreciated beautiful geometrical forms in the universe and tried to copy these in their own works, so that their monuments would fit into the plan of God's own mighty creation. The clay tablets record not only accounts of business transactions, but the patient observation of the stars. The Wise Men who came to worship our Lord in the manger were star-gazers who learned to look for the True Light, through many long nights in the desert marking the paths of the planets.
A permanent reminder of these days is our occasional use of the sexagesimal system (based on 60 rather than 102), which was often used in Mesopotamia. It is probable that this originated in the symbol of the year as a circle. Since the year has approximately 360 days, and these people knew that if we take the radius of a circle and use it as a chord it will form within the circle a regular hexagon (six-sided figure), they divided this year-circle into 0360 degrees, as we still do. Each hour of the day also was given 60 minutes, and each minute 60 seconds.
This interest in numbers as at once practical and symbolic spread from Mesopotamia and Egypt to all the lands which derived their civilization from them. In Europe in southern Italy it found a special student in Pythagoras. We do not know much about Pythagoras (although he has given his name to a famous theorem in geometry), but we do know that be founded a sort of religious order devoted to a strict life based on the idea of number and measure in all things. Perhaps their most important discovery was the theory of music, which shows that the relation of musical tones to each other is due to a ratio between tones (see pages 349 ff.).
The discoveries of Pythagoras stimulated a still greater Greek, namely, Plato, to make mathematics the basic study in his great school, called the Academy. Many of his pupils made basic advances in mathematics and in the application of mathematics to astronomy, but it was Aristotle whose invention of logic made it possible to turn mathematics into a true science. Science means not only to know that something is true, but to show why it must be true. The Babylonians and Egyptians had discovered many mathematical truths, but they had never demonstrated them, nor was this possible until Aristotle's discovery of logic.
This scientific approach to mathematics, based on principles, definitions, and proofs, made it possible to distinguish very clearly between three kinds of quantities:
- 1. Concrete quantity: 5 fingers, 5 horses, 6 bushels of wheat -- the accountant's
view of mathematics.
- 2. Abstract quantity: 5, 6, x, y, a plane, a solid. This is the pure mathematician's way of thinking of quantity.
- 3. Applied quantity: 5, 6, a circle, or square, used to count and measure less abstract quantities. This is the way we use mathematics in other sciences, for example, physics.
- 2. Abstract quantity: 5, 6, x, y, a plane, a solid. This is the pure mathematician's way of thinking of quantity.
Following Aristotle, mathematics was first organized and formulated in ancient times in the Elements of Euclid. Modern achievements in mathematics have been very great and are progressing rapidly today, but they are secure only when they rest on this ancient foundation.
WHY IS MATHEMATICS VALUABLE TODAY?
We have seen why the ancients valued mathematics so highly. Is it still of value? We may formulate the value of mathematics in the following outline:
A. Mathematics is valuable as a liberal art. The liberal arts are tools used by other subjects. Mathematics is a tool subject in two ways:
- 1. It is a necessary exercise in logical thinking.
- The great tool of all thought is logic (critical analysis). Logic teaches us four kinds of argument: poetic, rhetorical, dialectical, and demonstrative (see Introduction pp. 18 f.).
- The first three kinds of argument can be exercised by the student on any kind of material, but demonstration must be exact and hence it can only be practiced on material which the student understands perfectly. But a beginning student cannot understand perfectly the material of the other sciences. Only mathematics has material which is simple enough (the numbers and figures) that a beginner can see and understand it clearly. This is because mathematics is abstract, that is, it leaves out the complicated characteristics of real substances and considers only the pure quantity of things. That is why there have been great mathematical geniuses who were very young (e.g., Galois), but few very young men who have been masters in other sciences. Hence a student will never master the art of logical demonstration except by practicing it in mathematics.
- 2. It is an important instrument of the other sciences.
-
a. Natural science constantly uses mathematics, since the relations between
the quantities of natural things are easiest for us to discover. We know little
about astronomy or physics without mathematics.
- b. The fine arts use mathematics because the beauty of things is found especially in their proportions. Thus the theory of music, of poetic rhythm, of painting, sculpture, and architecture, all make use of mathematical principles.
- c. The social sciences use mathematics (statistics) because the complexities of social facts cannot be reduced to order without mathematics.
- d. All forms of engineering use mathematics for the same reason as the above sciences and arts.
- b. The fine arts use mathematics because the beauty of things is found especially in their proportions. Thus the theory of music, of poetic rhythm, of painting, sculpture, and architecture, all make use of mathematical principles.
- The great tool of all thought is logic (critical analysis). Logic teaches us four kinds of argument: poetic, rhetorical, dialectical, and demonstrative (see Introduction pp. 18 f.).
Mathematics is inferior to other pure sciences in the subject which it studies. Quantity is little compared with God whom theology studies, or with the physical universe which natural science studies. But it is better than logic, since logic studies relations that do not exist in reality. Yet mathematics is better than all other sciences in its certitude and clearness. For this reason it is valuable as a pure science, which it is delightful and enjoyable to know for its own sake.
We have said that mathematics is a liberal art, but this raises a problem. A servile art is one which makes some external, material product. A liberal art is one which makes something in our mind. How can mathematics make anything in our mind?
We make things in our mind by comparing, contrasting, combining, and separating the different things we know (objective concepts) in some kind of mental order by means of mental relations (see pages 454 f.). In this way we can construct a number in our minds. If I ask you to make a number greater than 1091, you can easily make 1091 + 1, although you have never experienced and could never live long enough to count so great a multitude of things. You can also construct figures. If I ask you to think of a line and then divide it into two parts which have the relation to each other of 1091: 1, you can do that, although you have never seen such a line.
We must understand, however, in what sense we "make" a number or magnitude. We can make in our mind a "dragon" or a "shmoo," even though such things do not exist anywhere, and, as far as we know, could not exist. We can also make in our mind the notion of a "square-circle," although we know positively that such a thing could not exist outside our mind. But the numbers and figures which we make do exist in reality in some way, namely, in the potentiality of matter.
There really are quantities in the world which we have experienced, and when we divide them mentally into any number of parts which we wish, or into any sort of figure, we are merely marking out mentally the parts which they really (but in a potential way) contain. Furthermore, we mark out these parts by using points to divide lines, and these lines to divide planes, and these planes to divide solids; and we produce numbers by counting these parts by the unit. The point and the unit which we use to mark out parts exist in real things, and the quantity which we divide is real and really contains these parts, although in a potential fashion. Hence although mathematics makes something in our mind, it does this only in order to study something which is real, and which we did not make, namely, quantity.
To be sure, in mathematics we do not consider quantity as it exists physically in this or that particular material thing. We consider it abstractly and as something which we imagine, but this abstraction is based on reality and is used to know reality.
Hence mathematics is different from logic, because logic studies mental relations which cannot exist outside our mind (for example: genus, difference, subject, predicate), while mathematics studies quantity which can really exist outside our mind, even though for purposes of study we construct it in our minds.* [* Some thinkers do not agree with this statement. We will explain their opinion below, page 395.]
Since mathematics as a liberal art is a perfect example and exercise in logical thinking, and as science is the clearest and most perfect of all, it must be taught and studied according to the laws of logic, as Aristotle and Euclid saw in establishing it as a science.
Logic teaches us three processes of thinking (see page 19).
- 1. Exact definition. We make an exact definition by classifying a thing. To classify
a thing we compare it to the class of things which are most like it. This is called
its genus. Then we contrast it to these other things by stating how it differs
from them. This is the difference.
- An exact definition, therefore, must be in terms of genus and difference by which the thing defined is located in a category. For example: a triangle is a polygon (genus) having three sides (difference) in the category of quality.
- It must also be noted that a definition may either explain the usage of some term (nominal definition), or the nature of something which is known to exist actually or possibly (real definition).
- 2. Exact statement: We must begin our mathematical reasoning with principles that are seen to be true from the quantities which we have experienced or can imagine. These principles are either:
- a. Axioms: principles which are common to more than one science, for
example, a whole is greater than any of its parts.
- b. Postulates: principles which are special or proper to one single science, for example, the definition of a straight line is proper to geometry, and the definition of the number 2 is proper to arithmetic.
- 3. Precise reasoning: We must prove our conclusions (theorems or answers to problems) by showing that they follow logically from our principles. Mathematical reasoning consists in being able to show that every conclusion is based on the axioms and the postulates. Mere ability to work problems does not prove that we are thinking mathematically; a machine can work problems, but it cannot tell why the answer is true.
- An exact definition, therefore, must be in terms of genus and difference by which the thing defined is located in a category. For example: a triangle is a polygon (genus) having three sides (difference) in the category of quality.
During the study of elementary algebra all these processes are used, but the first of them, exact definition, is usually stressed. In the remainder of this chapter we are going to develop some of the basic definitions used in algebra.
Arithmetic has been familiar to you from your first years in school. Algebra is something new, but not a new science. The name is from the Arabian, al-jebr; it is derived from the title of a book, Al-jebr w'al-muqâbalah, written by Mohammed, son of Moses of Kohwarezm (Al-Khowârizmî), in the city of Bagdad about 825 A.D. This book was very often used as a textbook in the Middle Ages. We are not sure exactly how the title should be translated. Some say that it means "restoration and equation," and others that both terms mean "equation," but that the first is an Arabic and the second a Persian term. In any case, it refers to the science of equations and their solution ("restoration"). The Arabians derived their knowledge of mathematics from Greek works preserved by the Christian peoples whom the armies of Islam had conquered.
Thus the actual knowledge of algebra goes clear back to the time of Euclid (about 350-300 B.C.), although by the Greeks it was simply called arithmetic, or the science of numbers. Arithmetic deals with equalities and inequalities between numbers (equations), but today we commonly use the term to refer to the elementary study of the subject, while we use the terms number theory and algebra to refer to a more advanced study of the same subject.
In arithmetic you have become familiar with the use of equations and of the familiar operations of addition, subtraction, multiplication, and division. These are also basic to the more advanced study which we call algebra, and to these we must add a less familiar notion, that of a class or set of numbers.
- Definition: A set of numbers is a collection of numbers having some common property that distinguishes them from other numbers.*
* Note that we speak here of a set of numbers, using "set" in a restricted sense. Ordinarily "set" means a collection of any kind of objects, called its "elements," whether these are numbers or not; the same restricted sense holds for the following definitions.For example, all odd numbers have the property of not being divisible into equal halves, and this makes them different from all other numbers, and all squares have the property of having equal numbers as their two factors; hence each collection is a set of numbers. In arithmetic we are used to dealing only with specific numbers --5, 21, 101, etc. -- but at the level of algebra we go on to consider such classes or sets of numbers. In order to have a notation for such sets of numbers, mathematicians in the 17th century invented literal numbers, just as the Hindus at an earlier period had invented our numbers 1, 2, 3, 4, etc., to stand for specific numbers. Thus we might use the letter a to stand for all odd numbers, and the letter b to stand for all even numbers, and the letter n to stand for some number, and we could write:
a = n + n, or a = 2n
b = n + n + 1, or b = 2n + l
The first equation would mean: "Every even number equals the sum of two equal parts"; and the second: "Every odd number when divided into its two greatest equal parts has a remainder of 1."
Many students are puzzled by this very logical system of notation. To understand it, they should remember that just as the word "man" stands not just for Peter, or for Paul, but for any and every man, so a literal number stands for any and every number of a certain set of numbers: it is a distributive universal term and not a singular term (see page 21). Used in this way, a literal number is said to stand for a variable, because it might mean any one of the set of numbers.
Frequently, however, we deal in algebra with two sets of numbers which have definite relations to each other, so that if we choose a number from set A, then we will find in set B another number which bears this relation to it. For example if we select any odd number from the set of odd numbers, we can find in the set of even numbers a number which is related to it by the relation "greater by 1." We call any such relation a function, and we say that the second number is a function of the first, and that it is a dependent variable, since it depends on our selection of the first number, The first number, since it is freely selected, is called the independent variable. Notice the following diagram:

Here are two sets of numbers. If we symbolize set A by the literal number x, and set B by the literal number y, then x and y are variables, because we may select any of the numbers in set A as the meaning of x, or in B, as the meaning of y. But if we consider the two sets as related to each other by a function, and consider x the independent variable, then if we select 3 as the meaning of x, we must select 9 as the meaning of y, y is said to be dependent on x, and to be its function. This can be expressed in the following equation:
which means that any x is related to some y as its square root. Thus we can state the following definition:
- Definition: A function is a set of ordered pairs of numbers such that no two pairs in the set can have the same first element and different second elements.
This means that we can consider A and B as a single set of numbers grouped in pairs having a definite relation to each other, so that once we have chosen one number we can be in no doubt as to its partner. Thus in algebra we are concerned not with specific numbers (3, 10, 21), but with sets of numbers, and our equations state relations or functions connecting two such sets:
| a=b2 × + y = z2 x2 + y2 = 0 |
In each case the two sides of the equation represent two sets of numbers related to each other by a definite function.
We have now seen that arithmetic treats of specific numbers, while algebra goes on to deal with classes of numbers and the relations between them. But what is a number? In algebra we will find that "number" is used today in a great many very different senses, that is, it is an analogical term (see page 50). Analogical terms are perfectly legitimate, but they are very dangerous if we begin confusing the different senses in which a term is used. Aristotle long ago took great care to remove the vague analogies used in mathematics before his time, especially by his fellow pupils in the school of Plato, and to replace them by careful distinctions of the senses of a. term, and by univocal definitions. Since number is the very subject-matter of algebra, we must begin algebra with a very clear notion of what a number is.
Some say that "number" is an "undefined term," but this need not be the case. A term can be defined if it can be located in a category (see page 59). If we ask the ten questions which mark out the categories (see page 45) we will see at once that numbers (5, 10, 21) answer the question, "How much or how many?" which is the characteristic of the category of quantity.
All the things that exist in the world which God has made from angels down to water and stones are in the category of substance. Each of these substances has many different characteristics, which we call its accidents (see page 44). Of these accidents the most basic one in the world of material substances is quantity.
Quantity, like all the names of the categories, really is an "undefined term," because it is only the things inside the categories which can properly be defined (see pp. 128 f.), but we can give a descriptive definition of it:
- Definition (descriptive): Quantity is the accident by which a substance has parts, each of which, if separated, would be another substance.
For example, a man has a definite quantity by which he has such parts as his head, trunk, arms, legs, hands, and feet. Each of these parts if cut off would still exist as separate (although non-living) substances. Similarly, if we pour fifteen glasses of milk from a full pitcher, we separate the original quantity (a "pitcher-full") into fifteen parts, each of which is a separate quantity of milk.
This is something very strange about quantity-namely, that it can be divided over and over again, and yet, no matter how small the parts, it is possible (in thought, at least) to imagine these as further divisible. We may say that quantity as quantity is potentially divisible to infinity, although it never is actually so divided, since at any moment it actually has a definite number of parts.
There are two kinds of quantity, magnitude and number.
- Definition: A magnitude, or continuous quantity, is a whole whose parts have position so that each part has a common boundary with another part.
- Definition: A point is the principle of magnitude, having position but no parts.
- Definition: A number, or discrete quantity, is a whole whose parts have no position or common boundary.
As the point is the principle of a magnitude but is not a magnitude, so the unit (symbolized by 1) is not a number (since it has no parts) but is a principle of number:
- Definition: A unit (1) is the principle of number, itself having no parts.
We have already said (page 307) that numbers can be concrete, abstract, or applied. Ordinarily when we apply an abstract number, we apply it to count the concrete things from which it was abstracted, but we can also use it to count spiritual things which in reality have no quantity since they have no matter. Thus we can speak of the existence of seven angels or of the three divine Persons, and these statements are true. Number used to count things without regard to whether they are material or immaterial is used in an analogical sense which transcends the categories.*
*Do not confuse this with the term "transcendental number" now used in mathematics to refer to pi and other similar quantities.
We have already noticed that we arrive at numbers by counting the parts of a magnitude. A magnitude is one quantity (a line, plane, or solid) and a number is one quantity. The magnitude has parts, each with a position and a boundary, and potentially divisible, and the number derived from this has corresponding parts without position and indivisible. To make a bigger number we can divide one of the parts of the magnitude by a point, line, or plane. This gives us a new number greater than the former number by a unit corresponding to the new part which has been marked off. All units in number are equal, since they are indivisible. Thus the species of numbers are determined by the ultimate unit. 2 is the discrete quantity or number formed by counting the parts of a magnitude which is once divided. 3 is the discrete quantity formed by counting the parts of a magnitude which is twice divided. This last definition is not circular, because we have already defined the notion of "twice" when we defined the number 2. Thus we are able to define any desired positive integer (the natural numbers) and to prove that it exists since it can be constructed.
The system of natural numbers is potentially infinite, that is, we can always construct a number greater than any given number. We could invent a new name and symbol or notation for every new number, but this would soon fill a dictionary. Hence men have invented different ways of naming and noting numbers by a small number of names and signs. Here are some of the systems that have been devised:
- 1. Simple grouping systems.
- A simple grouping system is a number system that consists of tally marks which are replaced by a group symbol when the tallies become too numerous. The Roman numerals form a simple grouping system of numbers.
- 2. Multiplicative grouping systems.
- This is an outgrowth of the simple system. There are special ciphers for the
numbers in the basic group, e.g., 1, 2, .... 9, and a special class of symbols for the
higher groups, e.g., t for 10, h for 100, th for 1000, etc.
- The ciphers are then used multiplicatively to show how many of the higher groups should be indicated. This leads to representations of the type: 3,297 equals 3 th and 2 h plus 9 t plus 7. The traditional Chinese-Japanese numeral system is a multiplicative grouping system.
- 3. Ciphered number systems.
- A third method of number writing may be called a ciphered numeral system. In the case of a decadic system one would denote the numbers from 1 to 9 by special symbols; similarly the multiples of 10 up to 90, the hundreds up to 900, and so on, would have their individual signs. All numbers can then be represented as a combination of such symbols in a very compact form. Egyptian and Greek number systems are usually ciphered.
- 4. Positional number systems.
- Positional number systems are based on the principle of local value, by which a
symbol designates a value or class which depends on the place it takes in the
numeral representation. Our decimal numeral system is a system of this type. For
instance, in the three numbers 352, 325, and 235, the digit 2 signifies respectively
2, 2 × 10, and 2 × 100.
- Positional number systems are closely related to the multiplicative grouping systems, and one obtains a positional system from a multiplicative grouping system simply by omitting the special symbols designating the higher class groups.
- The only complication which the positional notation involves lies in the necessity of introducing a zero symbol to express a void or missing class; for instance, it has to be shown that 204 is different from 24. The essential discovery in the positional system may be considered to lie in the invention of this symbol.
- The many advantages of the positional system are not difficult to perceive. First, the numeral notation is very compact and readable. Next, it is possible to express arbitrarily large numbers simply by the digits in the basic group. Finally, and most important, it is possible to invent simple rules for performing calculations (addition, multiplication, division) that can only be performed laboriously in other systems. Although our positional system uses 10 signs and is said to be "to the base ten," it is just as easy to have systems to other bases, let us say 2, or 12.
- Positional number systems are closely related to the multiplicative grouping systems, and one obtains a positional system from a multiplicative grouping system simply by omitting the special symbols designating the higher class groups.
Every number is a species within the genus of number. The difference by which each number is specified and defined is its last unit which makes it different from the number less than it (because greater by one part) and also different from the number greater than it (because this last unit is last). Thus 9 is greater than 8 by a unit, and less than 10, because that unit is its last, while 10 has still another unit.
There are many sub-genera or classes of numbers. Of these we can list the following interesting classes:
- 1. An even number is that which can be divided into two equal parts without a unit
intervening in the middle.
- a. Evenly even is a number which is capable of being divided into two equal parts
and with each of its parts similarly capable of division and so on until the unit is
reached. E.g.: 2, 4, 8, 16, 32, 64, 128, 256, 512.
- b. Oddly even is an even number, the halves of which are not immediately divisible into two equals. E.g.: 6, 10, 14, 18, 22, 26.
- c. Evenly odd is an even number which can be divided into two equal parts whose parts also can be so divided and sometimes even the parts of its parts, but it cannot carry the division of its parts as far as the unit. E.g.: 12, 24, 48, 96 etc; 20, 40, 80, 160, etc; 28, 56, 112, 224, etc.
- b. Oddly even is an even number, the halves of which are not immediately divisible into two equals. E.g.: 6, 10, 14, 18, 22, 26.
- 2. Odd numbers cannot be divided into two equal parts because a unit always occurs
in between.
- a. Prime numbers (2 is an exception, the only even prime number, why?).
- A prime is one that has no other factors than itself and the unit. (It is called prime because it is measured only by the unit or prime). E.g.: 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, etc.
- b. A composite number is a odd number that is factorable, or that is composed of parts other than the unit. E.g.: 9, 15, 21, 25, 27, 33, 35, 39, etc.
- A prime is one that has no other factors than itself and the unit. (It is called prime because it is measured only by the unit or prime). E.g.: 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, etc.
There are many other less fundamental classifications of numbers.
The natural numbers or positive integers are the only numbers in a strict and univocal sense. We have seen already that the unit and zero are sometimes called numbers in a wider sense. Besides these, in arithmetic we are familiar with the signs of operations by which we construct numbers: + , - , × , ÷ , < , x² etc. In algebra and higher branches of mathematics many other signs of operation are introduced. Furthermore, combinations of numbers and signs of operations are used and referred to as "numbers." These we may call artificial (in contrast to natural numbers) or operational numbers, understanding again that the word "number" applies to them only by analogy that is, by an extension or generalization of the concept.
We may list them as follows:
- 1. Zero. This stands for the operation of not taking a part in constructing a number,
Thus 100 means that we take 1 one-hundred, but no ten's, and no units in
constructing the number.
- 2. Negative numbers. These stand for the operation of counting in the reverse order, that is, in the direction of lesser numbers. Thus - 4 means four units which would have to be added in order to complete a given number. These were introduced in order to be able to perform the operation of subtraction when the number to be subtracted is greater than that from which it is subtracted.
- 3. Fractions. A fraction is not part of a unit, since a unit has no parts. It is a ratio between two numbers. Thus 3/4 is the ratio of 3 compared to 4. These were introduced in order to be able to perform operations of division when the divisor is not a factor of the dividend.
- 2. Negative numbers. These stand for the operation of counting in the reverse order, that is, in the direction of lesser numbers. Thus - 4 means four units which would have to be added in order to complete a given number. These were introduced in order to be able to perform the operation of subtraction when the number to be subtracted is greater than that from which it is subtracted.
The foregoing "numbers" along with the natural numbers form a collection, all of which can be added, subtracted, multiplied, and divided by each other (excluding division by zero however). Such a collection is called a field, and this field is named "the field of rational numbers," the term "rational" indicating that it includes fractions (ratios).
- Definition: A "set of numbers" is a field if it is possible to add, subtract, multiply, and divide any of these "numbers" by any other, excluding division by zero, without going outside the "set."
Notice that in this definition we have widened or generalized the notion of number and hence also of "set."
There remain, however, many equations which cannot be solved only with these
"numbers", for example, the equation ![]() Hence we add the following definition:
Hence we add the following definition:
- 4. Irrational numbers. An irrational number is the limit of two converging series of fractions (rational numbers). For example, in taking the square root of 2 (approximately 1.41421) we got closer and closer but never reach a value without a remainder. The limit is greater than 1.41421, but less than 1.41422, etc.
If we add irrational numbers to the field of rational numbers we get the field called "the real numbers." But still another type of "number" is necessary in order to solve all equations, If, in the equation x² = -2, we attempt to take the square root of -2, we find Ourselves in the difficulty that a negative number × gives a positive number; hence -2 cannot be the square of any number in the real number system. Therefore we add:
- 5. Imaginary numbers. An imaginary number indicates the process of taking an even root of a negative number. It is really no more "imaginary" than are negative numbers themselves.
This "set" of "numbers" is now sufficient to solve algebraic equations of any degree. How may we now give a univocal definition of the word "number" as we are now using it in such a wide sense? This is done by defining "number" as follows:
- Definition: "Number" (complex number) as used in algebra refers to a quantity
which can be constructed according to the following formula: a + b
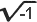 ,
where a and b are real numbers.
,
where a and b are real numbers.
For example, the number 3 can then be written as 3 + 0 ![]() , while the "imaginary number"
, while the "imaginary number" ![]() can be written as 0 + 1
can be written as 0 + 1 ![]() . Since we can give a single meaning to "number" taken in
this sense, it is a univocal definition. The system of all these "numbers" is called the
complex number system" and it forms a single field. This field of natural and artificial
numbers forms the subject matter of ordinary algebra, which seeks to study the different
relations between such complex numbers.
. Since we can give a single meaning to "number" taken in
this sense, it is a univocal definition. The system of all these "numbers" is called the
complex number system" and it forms a single field. This field of natural and artificial
numbers forms the subject matter of ordinary algebra, which seeks to study the different
relations between such complex numbers.
In elementary algebra the order of study is usually approximately as follows:
- A. Learning to translate arithmetical problems into literal numbers, and a review of
the basic operations of addition, subtraction, multiplication, and division.
- 1. The idea of number is clarified (as above) and the student learns to distinguish
between numbers and the system of notation of numbers. Then the use of
literal numbers, the nature of a variable, and of algebraic expressions (polynomials) are discussed. This pertains to the logical process of definition.
- 2. The Student learns how to perform the basic operations with algebraic numbers. This has to do with the logical process of statement, since the student is learning to translate one statement (equation) into another.
- 2. The Student learns how to perform the basic operations with algebraic numbers. This has to do with the logical process of statement, since the student is learning to translate one statement (equation) into another.
- B. The Solution of equations:
The foregoing has been introductory, since up to this point nothing has actually been proved or demonstrated, but the tools of demonstration have been prepared. The real science consists in demonstrations, the third logical process. - 1. Number theory: At this point it would be logical first of all to demonstrate the
various properties of sets of numbers, odd, even, prime, etc. Today this is
ordinarily omitted from elementary algebra courses, although among the
Greeks it formed the main part of arithmetic. It is a very beautiful part of the
science, but less practical in application.
- 2. Equations: Most of the time is devoted to studying the relations between sets of numbers, that is, algebraic functions. This study is ordered according to the complexity of the equations:
- a. Linear equations
- b. Quadratic equations
- c. Equations of higher degree.
- 2. Equations: Most of the time is devoted to studying the relations between sets of numbers, that is, algebraic functions. This study is ordered according to the complexity of the equations:
In this study of equations in elementary algebra, operations are stressed as in arithmetic. The main problem is construction of a number which satisfies a given equation. Actually this is not the main concern of mathematics as a science, which rather seeks to demonstrate that such a solution is valid according to the laws of the number system. This demonstrative study of mathematics is usually taken up only in the study of geometry; hence we will discuss algebra as strict science in the next chapter along with geometry.